Cho tam giác \(ABC\) có \(AB = 12\,\,{\rm{cm}}\,;\,\,AC = 15\,\,{\rm{cm}}\) và \(\widehat B = 60^\circ \). Độ dài cạnh \(BC\) bằng
Quảng cáo
Trả lời:
Chọn B
Kẻ đường cao \(AH.\)
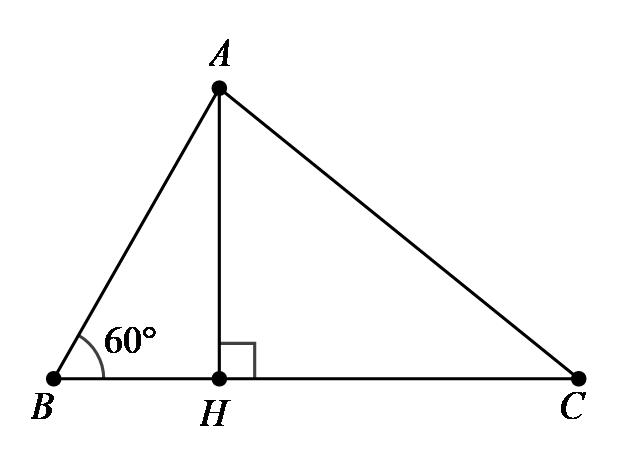
Xét tam giác vuông \(ABH\), ta có:
\[BH = AB \cdot \cos B = AB \cdot \cos 60^\circ = 12 \cdot \frac{1}{2} = 6\,\,({\rm{cm)}}{\rm{.}}\]
\(AH = AB \cdot \sin B = AB \cdot \sin 60^\circ = 12 \cdot \frac{{\sqrt 3 }}{2} = 6\sqrt 3 \,\,({\rm{cm)}}.\)
Áp dụng định lí Pythagore vào tam giác vuông \(AHC\), ta có: \(H{C^2} = A{C^2} - A{H^2} = {15^2} - {\left( {6\sqrt 3 } \right)^2} = 117\).
Suy ra \(HC = 3\sqrt {13} \,\,({\rm{cm)}}\).
Vậy \(BC = CH + HB = 3\sqrt {13} + 6\,\,({\rm{cm)}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
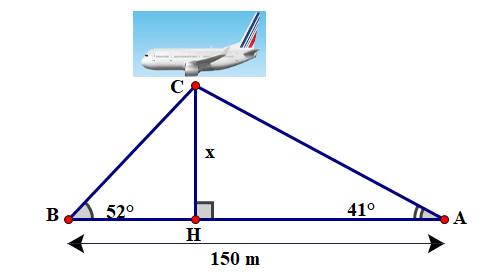
Đặt \(CH = x\,\,(\;{\rm{m}}),\,\,x > 0\).
• Xét \(\Delta HBC\) vuông tại \[H,\] ta có:
\(\tan \widehat {CBH} = \frac{{CH}}{{BH}}\) hay \(\tan 52^\circ = \frac{x}{{BH}}\) nên \(BH = \frac{x}{{\tan 52^\circ }}\).
• Xét \(\Delta HAC\) vuông tại \[H,\] ta có:
\(\tan \widehat {CAH} = \frac{{CH}}{{AH}}\) hay \(\tan 41^\circ = \frac{x}{{AH}}\) nên \(AH = \frac{x}{{\tan 41^\circ }}\).
Ta có: \(HB + HA = AB\)
\(\frac{x}{{\tan 52^\circ }} + \frac{x}{{\tan 41^\circ }} = 150\)
\(x\left( {\frac{1}{{\tan 52^\circ }} + \frac{1}{{\tan 41^\circ }}} \right) = 150\)
\[x = \frac{{150}}{{\frac{1}{{\tan 52^\circ }} + \frac{1}{{\tan 41^\circ }}}} \approx 78\;\,({\rm{m)}}.\]
Vậy độ cao máy bay là \[78{\rm{ m}}.\]
Đáp án: 78.
Lời giải
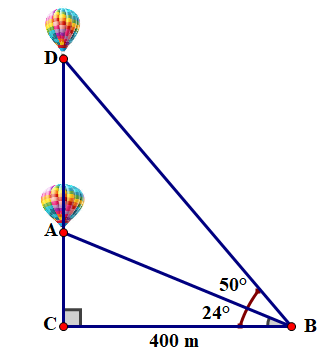
Xét \(\Delta ABC\) vuông tại \(B\), ta có:
\[\sin A = \frac{{BC}}{{AC}}\] hay \[\sin 24^\circ = \frac{{BC}}{{0,6}}\] nên \[BC = 0,6 \cdot \sin 24^\circ = 0,24\,\,({\rm{m}})\].
Vậy mặt bàn viết được nâng lên \(0,24\,\;{\rm{m}}{\rm{.}}\)
Đáp án: 0,24.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.