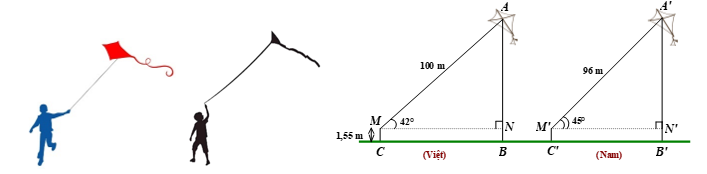
Hai bạn Việt và Nam cùng chơi thả diều trên một bãi đất phẳng, sợi dây diều của bạn Việt có độ dài \[100\,\,{\rm{m}}\] và dây diều tạo với phương ngang một góc \[{\rm{42}}^\circ \] còn sợi dây diều của bạn Nam có độ dài \[96\,\,{\rm{m}}\] và dây diều tạo với phương ngang một góc \[{\rm{45}}^\circ \]. Cho biết tầm mắt của cả hai bạn đều là \[1,55\,\,{\rm{m}}\] và coi các dây diều được thả hết và căng thẳng (tham khảo hình vẽ).
a) Diều của bạn Việt có độ cao so với mặt đất khoảng \[68,46\,\,{\rm{m}}.\]
b) So với mặt đất thì diều của bạn Nam có độ cao khoảng \[75,25\,\,{\rm{m}}.\]
c) Diều của bạn Nam lên cao hơn diều của bạn Việt.
d) So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[6,79\,\,{\rm{m}}{\rm{.}}\]
Hai bạn Việt và Nam cùng chơi thả diều trên một bãi đất phẳng, sợi dây diều của bạn Việt có độ dài \[100\,\,{\rm{m}}\] và dây diều tạo với phương ngang một góc \[{\rm{42}}^\circ \] còn sợi dây diều của bạn Nam có độ dài \[96\,\,{\rm{m}}\] và dây diều tạo với phương ngang một góc \[{\rm{45}}^\circ \]. Cho biết tầm mắt của cả hai bạn đều là \[1,55\,\,{\rm{m}}\] và coi các dây diều được thả hết và căng thẳng (tham khảo hình vẽ).

a) Diều của bạn Việt có độ cao so với mặt đất khoảng \[68,46\,\,{\rm{m}}.\]
b) So với mặt đất thì diều của bạn Nam có độ cao khoảng \[75,25\,\,{\rm{m}}.\]
c) Diều của bạn Nam lên cao hơn diều của bạn Việt.
d) So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[6,79\,\,{\rm{m}}{\rm{.}}\]
Quảng cáo
Trả lời:

Theo bài ra ta có \[MC = NB = 1,55\,\,{\rm{m}}\] và \[M'C' = N'B' = 1,55\,\,{\rm{m}}\].
a) Đúng. Tam giác \[ANM\] vuông tại \[N\] nên \[AN = AM.\sin M\].
So với mặt đất thì diều của bạn Việt có độ cao là \[AB = AN + NB\].
Do đó \[AB = 100\sin 42^\circ + 1,55 \approx 68,46\,\,\left( {\rm{m}} \right)\].
Vậy diều của bạn Việt có độ cao so với mặt đất khoảng \[68,46\,\,{\rm{m}}.\]
b) Sai. Tam giác \[A'N'M'\] vuông tại \[N'\] nên \[A'N' = A'M'.\sin M'\].
So với mặt đất thì diều của bạn Nam có độ cao là \[A'B' = A'N' + N'B'\].
Do đó \[A'B' = 96\sin 45^\circ + 1,55 \approx 69,43\,\,\left( {\rm{m}} \right).\]
Vậy so với mặt đất thì diều của bạn Nam có độ cao khoảng \[69,43\,\,{\rm{m}}.\]
c) Đúng. Vì\[A'B' > AB\], hay diều của bạn Nam lên cao hơn diều của bạn Việt.
d) Sai. So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn: \[69,43\, - 68,46\,\, = 0,97\,\,\left( {\rm{m}} \right)\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
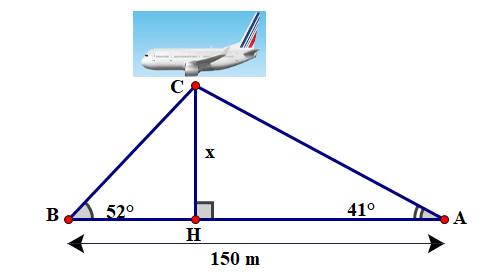
Đặt \(CH = x\,\,(\;{\rm{m}}),\,\,x > 0\).
• Xét \(\Delta HBC\) vuông tại \[H,\] ta có:
\(\tan \widehat {CBH} = \frac{{CH}}{{BH}}\) hay \(\tan 52^\circ = \frac{x}{{BH}}\) nên \(BH = \frac{x}{{\tan 52^\circ }}\).
• Xét \(\Delta HAC\) vuông tại \[H,\] ta có:
\(\tan \widehat {CAH} = \frac{{CH}}{{AH}}\) hay \(\tan 41^\circ = \frac{x}{{AH}}\) nên \(AH = \frac{x}{{\tan 41^\circ }}\).
Ta có: \(HB + HA = AB\)
\(\frac{x}{{\tan 52^\circ }} + \frac{x}{{\tan 41^\circ }} = 150\)
\(x\left( {\frac{1}{{\tan 52^\circ }} + \frac{1}{{\tan 41^\circ }}} \right) = 150\)
\[x = \frac{{150}}{{\frac{1}{{\tan 52^\circ }} + \frac{1}{{\tan 41^\circ }}}} \approx 78\;\,({\rm{m)}}.\]
Vậy độ cao máy bay là \[78{\rm{ m}}.\]
Đáp án: 78.
Lời giải
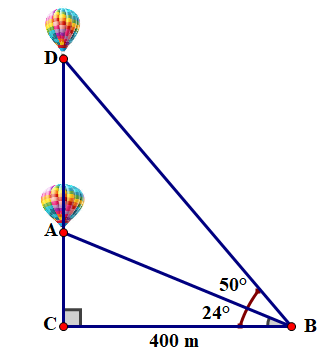
Xét \(\Delta ABC\) vuông tại \(B\), ta có:
\[\sin A = \frac{{BC}}{{AC}}\] hay \[\sin 24^\circ = \frac{{BC}}{{0,6}}\] nên \[BC = 0,6 \cdot \sin 24^\circ = 0,24\,\,({\rm{m}})\].
Vậy mặt bàn viết được nâng lên \(0,24\,\;{\rm{m}}{\rm{.}}\)
Đáp án: 0,24.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.