PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - m{x^2} + \left( {4\;m - 2} \right)x + 1 - 4\;m}}{{x - 1}}\) có đồ thị là \(\left( C \right)\) với \(m\) là tham số
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số không cắt trục \(Ox\).
c) Khi \[m < - 1\] thì hàm số đạt cực đại và cực tiểu trong miền \(x > 0\).
d) Có 2 phương trình tiếp tuyến của \(\left( C \right)\) song song với đường thẳng \(x - y = 0\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - m{x^2} + \left( {4\;m - 2} \right)x + 1 - 4\;m}}{{x - 1}}\) có đồ thị là \(\left( C \right)\) với \(m\) là tham số
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số không cắt trục \(Ox\).
c) Khi \[m < - 1\] thì hàm số đạt cực đại và cực tiểu trong miền \(x > 0\).
d) Có 2 phương trình tiếp tuyến của \(\left( C \right)\) song song với đường thẳng \(x - y = 0\).
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
|
a) |
Đ |
b) |
Đ |
c) |
Đ |
d) |
Đ |
(a) Đúng: Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị
(b) Đúng: Khi \(m = 1:y = \frac{{ - {x^2} + 2x - 3}}{{x - 1}} = - x + 1 - \frac{2}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\);
\(y' = \frac{{ - {x^2} + 2x + 1}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow - {x^2} + 2x + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1 - \sqrt 2 \Rightarrow y = 2\sqrt 2 }\\{x = 1 + \sqrt 2 \Rightarrow y = - 2\sqrt 2 }\end{array}} \right.\)
\(\mathop {\lim }\limits_{x \to 1 \pm } y = \pm \infty :x = 1\)là tiệm cận đứng; \(\mathop {\lim }\limits_{x \to \pm x} y = - x + 1:y = - x + 1\) là tiệm cận xiên
Bảng biến thiên:
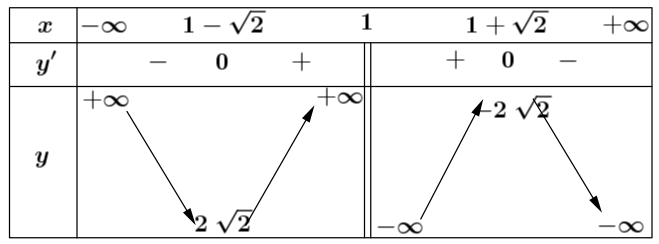
\(x = 0 \Rightarrow y = 3\); \(y = 0 \Rightarrow - {x^2} + 2x - 3 = 0\) (vô nghiệm) nên đồ thị hàm số không cắt trục \(Ox\)
(c) Đúng: \(y = \frac{{ - m{x^2} + \left( {4m - 2} \right)x + 1 - 4m}}{{x - 1}} \Rightarrow y' = \frac{{ - m{x^2} + 2mx - 4m + 2 - 1 + 4m}}{{{{\left( {x - 1} \right)}^2}}}\)
Suy ra \(y' = \frac{{ - m{x^2} + 2mx + 1}}{{{{\left( {x - 1} \right)}^2}}}\). Dấu \(y'\) là dấu của tam thức \(g\left( x \right) = - m{x^2} + 2mx + 1\)
\(g\left( x \right){\rm{ c\'o }}\Delta ' = {m^2} + m\,;\,\,g\left( 1 \right) = - m + 2m + 1 = m + 1\)
Để hàm số có cực đại và cực tiểu thì \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{m + 1 \ne 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < - 1}\\{m > 0}\end{array}} \right.} \right.\)
Lúc này hàm số đạt cực đại và cực tiểu tại \(x = {x_1},x = {x_2}\) và \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2}\\{{x_1} \cdot {x_2} = - \frac{1}{m}}\end{array}} \right.\).
Giả sử \({x_1} < {x_2}\)
Theo yêu cầu bài toán: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} > 0}\\{{x_2} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} > 0}\\{{x_1} \cdot {x_2} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2 > 0{\rm{ (lu\^o n d\'u ng) }}}\\{ - \frac{1}{m} > 0}\end{array} \Leftrightarrow m < 0} \right.} \right.} \right.\)
Giao với điều kiện \(\Delta ' > 0\) được \(m < - 1\)
(d) Đúng: \({y'_x} = \frac{{ - {x^2} + 2x + 1}}{{{{\left( {x - 1} \right)}^2}}}\). Đường thẳng \(x - y = 0\) có hệ số góc \(k = 1\)
Để tiếp tuyến của \(\left( C \right)\) song song với đường thẳng \(y = x\) cần và đủ là \({y'_x} = 1\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{\frac{{ - {x^2} + 2x + 1}}{{{{\left( {x - 1} \right)}^2}}} = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{ - {x^2} + 2x + 1 = {x^2} - 2x + 1}\end{array}} \right.} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{2{x^2} - 4x = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow y = 3}\\{x = 2 \Rightarrow y = - 3}\end{array}} \right.} \right.\)
Có hai tiếp tuyến thỏa yêu cầu bài toán:
\(\left( {{T_1}} \right):y = 1\left( {x - 0} \right) + 3 \Leftrightarrow y = x + 3\,;\,\,\left( {{T_2}} \right):y = 1\left( {x - 2} \right) - 3 \Leftrightarrow y = x - 5\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
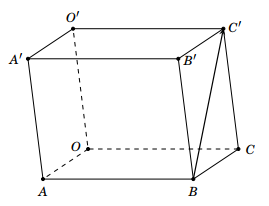
(a) Đúng: Gọi \(C'\left( {x;y;z} \right)\). Ta có \(\overrightarrow {BC'} = \left( {2; - 6;6} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x - 0 = 2}\\{y - 3 = - 6}\\{z - 0 = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = - 3}\\{z = 6}\end{array}} \right.} \right.\)\( \Rightarrow C\left( {2; - 3;6} \right)\).
(b) Đúng: Gọi \(O'\left( {x;y;z} \right)\). Theo hình vẽ thì \(\overrightarrow {AO'} = \overrightarrow {BC'} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x - 1 = 2}\\{y - 1 = - 6}\\{z + 1 = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = - 5}\\{z = 5}\end{array}} \right.} \right.\)\( \Rightarrow O'\left( {3; - 5;5} \right)\)
(c) Sai: Theo hình vẽ thì \(\overrightarrow {AB'} = \overrightarrow {OC'} = \left( {2; - 3;6} \right)\).
(d) Sai: Ta có \(\overrightarrow {HK} = \overrightarrow {AB} = \left( { - 1;2;1} \right)\).
Lời giải
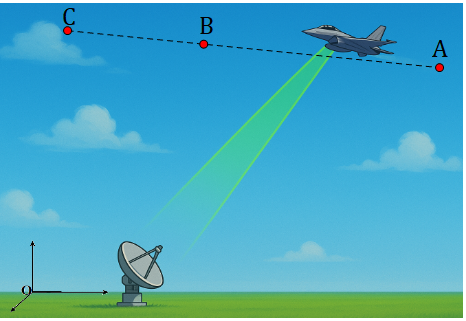
Do máy bay giữ nguyên tốc độ nên vận tốc của máy bay trên quãng đường \[AB\] và \[BC\] là như nhau. Ta có: \[\frac{{AB}}{{10}} = \frac{{BC}}{5} \Leftrightarrow AB = 2BC\].
Và máy bay giữ nguyên hướng bay nên hai vectơ \[\overrightarrow {AB} ;\,\overrightarrow {BC} \] cùng hướng.
Do đó \[\overrightarrow {AB} = 2\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}140 = 2\left( {x - 940} \right)\\50 = 2\left( {y - 550} \right)\\2 = 2\left( {z - 9} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1010\\y = 575\\z = 10\end{array} \right.\]
Vậy \[x\, + \,y\, + z = 1595\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.