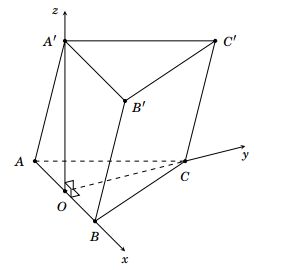
Cho 3 điểm \(M\left( {2;0;0} \right)\), \(N\left( {0; - 3;0} \right)\), \(P\left( {0;0;4} \right)\). Nếu \[MNPQ\] là hình bình hành thì tọa độ của điểm \(Q\) là
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Chọn D
Ta có: \(\overrightarrow {NP} = \left( {0;3;4} \right)\); \(\overrightarrow {MQ} = \left( {{x_Q} - 2;{y_Q};{z_Q}} \right)\)
\[MNPQ\] là hình bình hành khi \(\overrightarrow {MQ} = \overrightarrow {NP} \)\( \Rightarrow \left\{ \begin{array}{l}{x_Q} = 2\\{y_Q} = 3\\{z_Q} = 4\end{array} \right.\).
Vậy tọa độ của điểm \(Q\left( {2;3;4} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
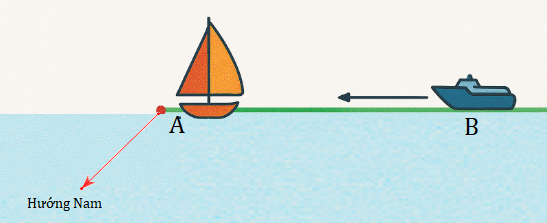
Quãng đường con tàu \(A\) đi được sau \(t\) giờ là: \(6t\) (hải lý)
Quãng đường con tàu \(B\) đi được sau \(t\) giờ là: \(8t\) (hải lý)
Sau \(t\) giờ khoảng cách giữa hai con tàu là:
\(f(t) = \sqrt {{{\left( {6t} \right)}^2} + {{\left( {10 - 8t} \right)}^2}} = \sqrt {100{t^2} - 160t + 100} = \sqrt {{{(10t - 8)}^2} + 36} \ge 6\)
Khoảng cách giữa hai con tàu ngắn nhất bằng \(6\)(hải lý) khi \(t = \frac{4}{5} = 0,8\) (giờ)
Vậy sau \(0,8\) giờ thì khoảng cách giữa hai con tàu ngắn nhất.
Lời giải
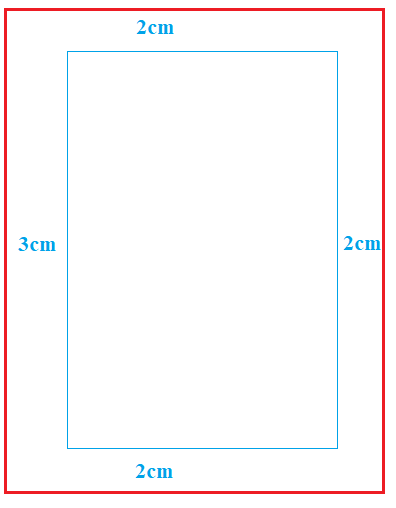
Gọi chiều dài của trang giấy là \(x\,cm\) ta có chiều rộng là \(\frac{{600}}{x}cm\).
Chiều dài và chiều rộng của phần in chữ lần lượt là \(x - 4\) và \(\frac{{600}}{x} - 5\)
Diện tích phần in chữ là \(f\left( x \right) = \left( {\frac{{600}}{x} - 5} \right)\left( {x - 4} \right) = 620 - 5x - \frac{{2400}}{x}\)
\(f'\left( x \right) = \frac{{2400}}{{{x^2}}} - 5 = 0 \Leftrightarrow x = \pm 4\sqrt {30} \)
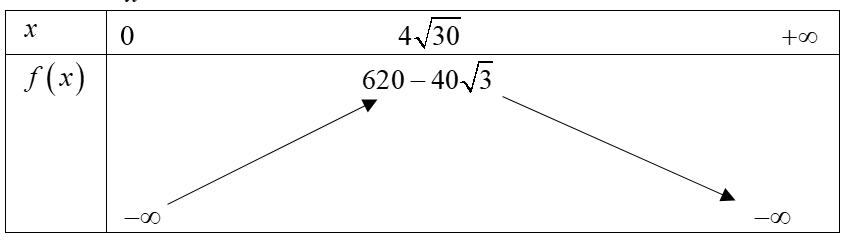
Vậy diện tích lớn nhất của phần in chữ xấp xỉ 401 \(c{m^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.