PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Một trang trại cần thuê xe để vận chuyển một lúc 120 con bò sữa và 30 tấn thức ăn cho bò. Nơi cho thuê xe chỉ có 9 chiếc xe loại lớn và 10 chiếc xe loại nhỏ. Một chiếc xe lớn chỉ có thể chở được 15 con bò và 5 tấn thức ăn. Một chiếc xe nhỏ chỉ có thể chở 12 con bò và 2 tấn thức ăn. Giá thuê của một chiếc xe lớn là 500 nghìn đồng và một chiếc xe nhỏ là 350 nghìn đồng. Hỏi chủ trang trại cần thuê xe với chi phí thấp nhất là bao nhiêu nghìn đồng?
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Một trang trại cần thuê xe để vận chuyển một lúc 120 con bò sữa và 30 tấn thức ăn cho bò. Nơi cho thuê xe chỉ có 9 chiếc xe loại lớn và 10 chiếc xe loại nhỏ. Một chiếc xe lớn chỉ có thể chở được 15 con bò và 5 tấn thức ăn. Một chiếc xe nhỏ chỉ có thể chở 12 con bò và 2 tấn thức ăn. Giá thuê của một chiếc xe lớn là 500 nghìn đồng và một chiếc xe nhỏ là 350 nghìn đồng. Hỏi chủ trang trại cần thuê xe với chi phí thấp nhất là bao nhiêu nghìn đồng?
Quảng cáo
Trả lời:
Trả lời: 3750
Gọi số xe lớn và số xe nhỏ mà chủ trang trại cần thuê lần lượt là \(x,y\left( {x,y \in \mathbb{N}} \right)\).
Theo đề ta có hệ bất phương trình \(\left\{ \begin{array}{l}15x + 12y \ge 120\\5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}5x + 4y - 40 \ge 0\\5x + 2y - 30 \ge 0\\0 \le x \le 9\\0 \le y \le 10\end{array} \right.\).
Biểu diễn tập nghiệm trên mặt phẳng tọa độ là
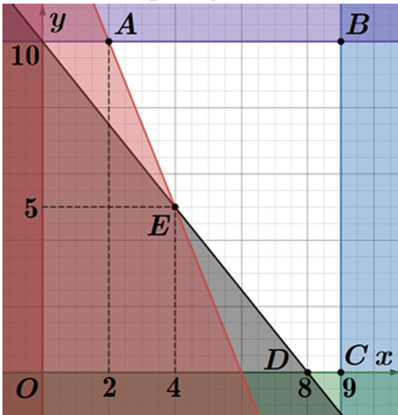
Khi đó miền nghiệm của hệ bất phương trình là miền trong của ngũ giác \(ABCDE\) (kể cả bờ) trong đó \(A\left( {2;10} \right),B\left( {9;10} \right),C\left( {9;0} \right),D\left( {8;0} \right),E\left( {4;5} \right)\).
Theo đề bài, ta có biểu thức biểu thị số tiền thuê xe là \(F\left( {x;y} \right) = 500x + 350y\) (nghìn đồng).
Ta có \(F\left( {2;10} \right) = 4500,F\left( {9;10} \right) = 8000,F\left( {9;0} \right) = 4500,F\left( {8;0} \right) = 4000,F\left( {4;5} \right) = 3750\).
Vậy số tiền thuê thấp nhất để chở 120 con bò sữa và 30 tấn thức ăn cho bò là 3750 nghìn đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 2
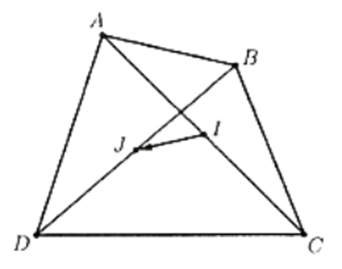
Ta có \(\left\{ \begin{array}{l}\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AB} + \overrightarrow {BJ} \\\overrightarrow {IJ} = \overrightarrow {IC} + \overrightarrow {CD} + \overrightarrow {DJ} \end{array} \right.\).
Cộng theo vế ta được
\(2\overrightarrow {IJ} = \left( {\overrightarrow {IA} + \overrightarrow {IC} } \right) + \left( {\overrightarrow {AB} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {BJ} + \overrightarrow {DJ} } \right)\)\( \Leftrightarrow 2\overrightarrow {IJ} = \overrightarrow {AB} + \overrightarrow {CD} \).
Suy ra \(k = 2\).
Câu 2
A. \(\left| {\overrightarrow {AO} } \right| = \frac{{a\sqrt 3 }}{2}\).
Lời giải
Đáp án đúng là: A
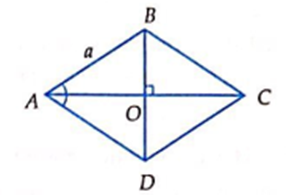
Vì \(\widehat A = 60^\circ \Rightarrow \Delta ABC\) đều \( \Rightarrow AO = \frac{{a\sqrt 3 }}{2} \Rightarrow \left| {\overrightarrow {AO} } \right| = \frac{{a\sqrt 3 }}{2}\)
Câu 3
A. \[\frac{a}{{\sin A}} = 2R\,.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[0,001\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.