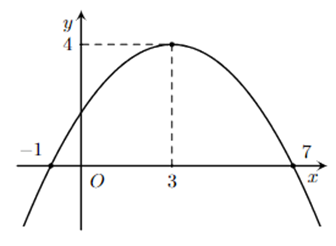Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y - 1 \ge 0\\2x + y - 3 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\) (I). Các câu sau đúng hay sai?
a) Đây là hệ bất phương trình bậc nhất hai ẩn.
b) \(\left( {3;2} \right)\) là một nghiệm của hệ bất phương trình.
c) Miền nghiệm của hệ bất phương trình trên là một miền tứ giác.
d) \(x = 1;y = 0\) là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x - y\) đạt giá trị nhỏ nhất.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y - 1 \ge 0\\2x + y - 3 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\) (I). Các câu sau đúng hay sai?
a) Đây là hệ bất phương trình bậc nhất hai ẩn.
b) \(\left( {3;2} \right)\) là một nghiệm của hệ bất phương trình.
c) Miền nghiệm của hệ bất phương trình trên là một miền tứ giác.
d) \(x = 1;y = 0\) là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x - y\) đạt giá trị nhỏ nhất.
Quảng cáo
Trả lời:
a) Đ, b) S, c) Đ, d) S
a) Đây là hệ bất phương trình bậc nhất hai ẩn.
b) Thay cặp số \(\left( {3;2} \right)\) vào bất phương trình thứ 2 của hệ ta thấy không thỏa mãn. Do đó \(\left( {3;2} \right)\) không là nghiệm của hệ bất phương trình.
c) Miền nghiệm của bất phương trình trên là miền tứ giác ABCD (phần tô màu).
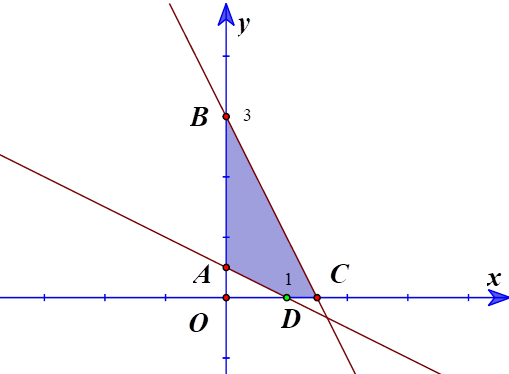
d) Ta có \(A\left( {0;\frac{1}{2}} \right),B\left( {0;3} \right),C\left( {\frac{3}{2};0} \right),D\left( {1;0} \right)\).
\(F\left( {0;\frac{1}{2}} \right) = 3.0 - \frac{1}{2} = - \frac{1}{2}\); \(F\left( {0;3} \right) = 3.0 - 3 = - 3\); \(F\left( {\frac{3}{2};0} \right) = 3.\frac{3}{2} - 0 = \frac{9}{2}\);
\(F\left( {1;0} \right) = 3.1 - 0 = 3\).
Do đó \(x = 0;y = 3\) là nghiệm của hệ bất phương trình (I) để \(F = 3x - y\) đạt giá trị nhỏ nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 2,18
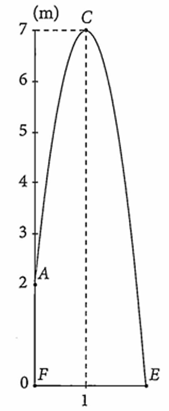
Giả sử gốc tọa độ tại điểm F.
Hàm số của đồ thị biểu diễn đường đi của viên bi có dạng \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\).
Theo hình vẽ ta có đồ thị có đỉnh là \(C\left( {1;7} \right)\) và đi qua điểm \(A\left( {0;2} \right)\) nên ta có:
\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a + b + c = 7\\c = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b + c = 7\\c = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 5\\b = 10\\c = 2\end{array} \right.\).
Do đó, đồ thị hàm số biểu diễn đường đi của viên bi là \(y = - 5{x^2} + 10x + 2\).
Điểm E là giao điểm của đồ thị với trục hoành nên hoành độ của điểm E là nghiệm của phương trình \( - 5{x^2} + 10x + 2 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5 + \sqrt {35} }}{5}\\x = \frac{{5 - \sqrt {35} }}{5}\end{array} \right.\).
Mà \({x_E} > 0\) nên \({x_E} = \frac{{5 + \sqrt {35} }}{5} \approx 2,18\).
Vậy khoảng cách từ vị trí E đến vị trí F khoảng 2,18 mét.
Câu 2
A. \(y = - {x^2} + 4x - 3\) .
B. \(y = {x^2} - 4x + 7\).
C. \(y = 2{x^2} - 12x + 20\).
Lời giải
Đáp án đúng là: D
Hàm số có giá trị lớn nhất bằng 3 tại \(x = 2\) suy ra \(a < 0\). Loại B, C.
Hàm số đi qua điểm \(\left( {2;3} \right)\) và \(\left( {1;0} \right)\). Chọn D.
Câu 3
A. \(\emptyset \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\).
B. \(\left( P \right)\) có đỉnh là \(I\left( {3;4} \right)\).
C. \(\left( P \right)\) cắt trục tung tại điểm có tung độ bằng 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(S = \frac{1}{2}bc\sin A\,.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.