Một nhà kho có dạng khối hộp chữ nhật cùng phần mái phía trên được thiết kế dạng vòm cong. Chiều dài của nhà kho là 40 m, chiều rộng 10 m, chiều cao 5 m; đường cắt của mái vòm khi cắt bởi mặt phẳng vuông góc với chiều dài của kho là một cung tròn, điểm cao nhất của mái vòm có chiều cao là 6 m (hình vẽ minh họa).
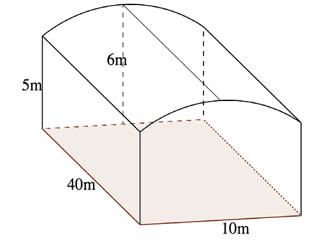
Để tính toán công suất cho hệ thống làm lạnh nhà kho, người ta cần ước lượng thể tích phần không gian bên trong nhà kho. Hãy cho biết thể tích không gian bên trong nhà kho là bao nhiêu mét khối (kết quả làm tròn đến hàng đơn vị)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
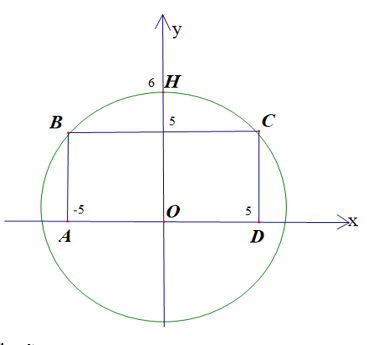
Gắn hệ trục Oxy như hình vẽ.
Phần mái của nhà kho là một phần của đường tròn \(\left( C \right)\) có phương trình:
\({x^2} + {y^2} + ax + by + c = 0\).
Vì \(\left( C \right)\) đi qua các điểm \(B\left( { - 5;5} \right),C\left( {5;5} \right),H\left( {0;6} \right)\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}25 + 25 - 5a + 5b + c = 0\\25 + 25 + 5a + 5b + c = 0\\36 + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 5a + 5b + c = - 50\\5a + 5b + c = - 50\\6b + c = - 36\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 14\\c = - 120\end{array} \right.\).
\( \Rightarrow \left( C \right):{x^2} + {y^2} + 14y - 120 = 0 \Leftrightarrow {x^2} + {\left( {y + 7} \right)^2} = 169 \Leftrightarrow \left[ \begin{array}{l}y = \sqrt {169 - {x^2}} - 7\\y = - \sqrt {169 - {x^2}} - 7\end{array} \right.\).
Vậy thể tích không gian bên trong nhà kho là:
\[V = S \cdot h = \left[ {\int\limits_{ - 5}^5 {\left( {\sqrt {169 - {x^2}} - 7} \right){\rm{d}}x} } \right] \cdot 40 \approx 2269\,\,{\rm{(}}{{\rm{m}}^{\rm{3}}}{\rm{)}}\].
Đáp án: 2269.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
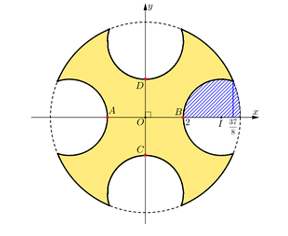
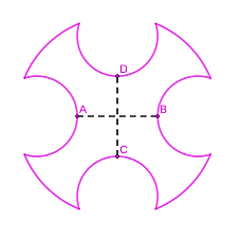
Chọn hệ trục \[Oxy\] sao cho gốc toạ độ \[O\] trùng với giao điểm \[AB,CD\].
Đường tròn lớn có phương trình: \[{x^2} + {y^2} = 25 \Rightarrow y = \pm \sqrt {25 - {x^2}} \].
Ta có \[OA = OB = OC = OD = \frac{4}{2} = 2\].
Đường tròn nhỏ có tâm trên trục \[Ox\]là \[\left( {4;0} \right)\] nên có phương trình:
\[{\left( {x - 4} \right)^2} + {y^2} = 4 \Rightarrow y = \pm \sqrt {4 - {{\left( {x - 4} \right)}^2}} \].
Ta có: \[\sqrt {25 - {x^2}} = \sqrt {4 - {{\left( {x - 4} \right)}^2}} \Leftrightarrow x = \frac{{37}}{8}\].
Gọi \(H\) là phần hình phẳng gạch chéo.
Ta có hình phẳng \(H\) giới hạn bởi các đường \[y = \sqrt {25 - {x^2}} ,y = \sqrt {4 - {{\left( {x - 4} \right)}^2}} ,y = 0\].
Đặt \({H_1} = \left\{ {y = \sqrt {4 - {{\left( {x - 4} \right)}^2}} ,y = 0,x = 2,x = \frac{{37}}{8}} \right\}\); \({H_2} = \left\{ {y = \sqrt {25 - {x^2}} ,y = 0,x = \frac{{37}}{8},x = 5} \right\}\).
Diện tích của hình \({H_1}\) là \[{S_{{H_1}}} = \int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x\].
Diện tích của hình \({H_2}\)là \({S_{{H_2}}} = \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x\).
Khi đó diện tích của hình \(H\) là: \[{S_H} = \int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x\].
Diện tích của đường tròn lớn là: \({S_1} = \pi \cdot {5^2} = 25\pi \).
Diện tích phần sơn 1 mặt của chi tiết máy
\[S = 25\pi - 8{S_H} = 25\pi - 8\left( {\int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x} \right) \approx 39,7\,({\rm{d}}{{\rm{m}}^{\rm{2}}}) = 0,397({{\rm{m}}^{\rm{2}}})\].
Chi phí để sơn hoàn thiện chi tiết máy: \[2 \cdot 0,397 \cdot 82 \approx 65\] (nghìn đồng).
Đáp án: 65.
Lời giải
a) Sai. Ta có \[h\left( t \right) = \int {v\left( t \right){\rm{dt}} = - 0,04{t^3} + 0,6{t^2} + C} \].
Tại thời điểm xuất phát \(\left( {t = 0} \right)\), độ cao của khinh khí cầu là 520 m nên
\[h\left( 0 \right) = 520 \Rightarrow C = 520\].
Vậy \[h\left( t \right) = - 0,04{t^3} + 0,6{t^2} + 520\].
b) Đúng. Tại thời điểm \(t = 3\) phút, độ cao của khinh khí cầu là \(h\left( 3 \right) = 524,32\) m.
c) Đúng. Ta có \(h'\left( t \right) = v\left( t \right) = - 0,12{t^2} + 1,2t\), suy ra \(h'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 10\end{array} \right.\).
Ta có bảng biến thiên:
Vậy độ cao tối đa của khinh khí cầu là 540 m.
d) Đúng. Khi trở lại độ cao như lúc xuất phát thì
\(h\left( t \right) = 520 \Leftrightarrow - 0,04{t^3} + 0,6{t^2} + 520 = 520 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 15\end{array} \right.\).
Vậy sau 15 phút thì khinh khí cầu quay trở lại độ cao như lúc đầu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập