Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), tam giác \(SAB\) là tam giác cân và nằm trong mặt phẳng vuông góc với đáy, gọi \(H\) là trung điểm cạnh \(AB\), khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCD} \right)\) là \(a\sqrt 2 \), gọi \(\alpha \) là góc giữa đường thẳng \(SD\) và mặt phẳng đáy. Tính giá trị của biểu thức \[M = 25{\tan ^2}\alpha + 4{\cot ^2}\alpha \].
Câu hỏi trong đề: Đề ôn luyện Toán Chương 5. Hình học không gian (đề số 1) !!
Quảng cáo
Trả lời:
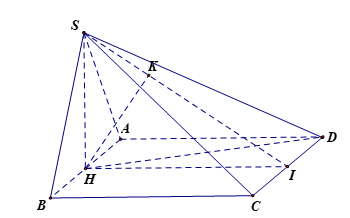
Gọi \(I\) là trung điểm \(CD\). Khi đó, ta có \(HI{\rm{//}}AD{\rm{//}}BC \Rightarrow HI \bot AB,\,\,HI \bot CD\).
Ta lại có tam giác \(SAB\) đều nên \(SH \bot AB\).
Mặt khác \(\left( {SAB} \right) \bot \left( {ABCD} \right)\), suy ra \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot HI\).
Kẻ \(HK \bot SI\,\,\left( {K \in SI} \right)\).
Ta có \(CD \bot HI\) và \(CD \bot SH\) \(\left( {{\rm{do}}\,SH \bot \left( {ABCD} \right)} \right)\).
Suy ra \(CD \bot \left( {SHI} \right) \Rightarrow CD \bot HK\).
Từ đó suy ra \(HK \bot \left( {SCD} \right) \Rightarrow d\left( {H,\left( {SCD} \right)} \right) = HK\).
Lại có \(BH{\rm{//}}CD \Rightarrow BH{\rm{//}}\left( {SCD} \right) \Rightarrow d\left( {B,\left( {SCD} \right)} \right) = d\left( {H,\left( {SCD} \right)} \right) = HK = a\sqrt 2 \).
Ta có \(HI = BC = 2a\).
Tam giác \(SHI\) vuông tại \(H\) nên ta có
\(\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} \Rightarrow \frac{1}{{S{H^2}}} = \frac{1}{{H{K^2}}} - \frac{1}{{H{I^2}}} = \frac{1}{{2{a^2}}} - \frac{1}{{4{a^2}}} = \frac{1}{{4{a^2}}} \Rightarrow SH = 2a\).
Vì \(SH \bot \left( {ABCD} \right)\) và \(SD\) cắt mặt phẳng \(\left( {ABCD} \right)\) tại \(D\)
\( \Rightarrow HD\) là hình chiếu của \(SD\) trên mặt phẳng \(\left( {ABCD} \right)\).
\( \Rightarrow \left( {SD,\left( {ABCD} \right)} \right) = \left( {SD,HD} \right) = \widehat {SDH}\).
Xét \(\Delta SHD\) vuông tại \(H\): \(\tan \widehat {SDH} = \frac{{SH}}{{HD}} = \frac{{2a}}{{a\sqrt 5 }} = \frac{2}{{\sqrt 5 }} \Rightarrow \cot \widehat {SDH} = \frac{{\sqrt 5 }}{2}\).
Vậy \[M = 25{\tan ^2}\alpha + 4{\cot ^2}\alpha = 25 \cdot {\left( {\frac{2}{{\sqrt 5 }}} \right)^2} + 4 \cdot {\left( {\frac{{\sqrt 5 }}{2}} \right)^2} = 25\].
Đáp án: 25.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
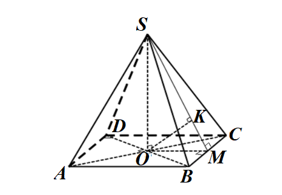
\(\left. \begin{array}{l}BC \bot OM\\BC \bot SO\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow BC \bot \left( {SOM} \right)\). Mà \(OK \subset \left( {SOM} \right) \Rightarrow BC \bot OK\).
Lại có \(SM \bot OK \Rightarrow OK \bot \left( {SBC} \right)\). Do đó \(d\left( {O,\left( {SBC} \right)} \right) = OK\). Chọn A.
Lời giải
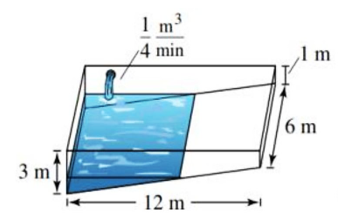
Xét các điểm như hình vẽ.
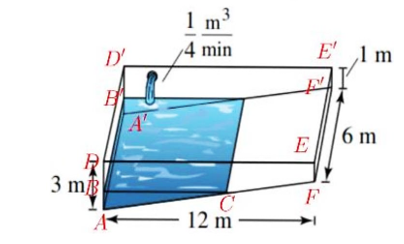
Ta có \(\frac{{BC}}{{DE}} = \frac{{AB}}{{AD}} \Rightarrow BC = \frac{{AB \cdot DE}}{{AD}} = \frac{{1 \cdot 12}}{3} = 4{\rm{\;}}\left( {\rm{m}} \right)\).
Khi mặt hồ phẳng lặng, phần nước đã có trong hồ bơi có dạng hình lăng trụ đứng tam giác.
\({S_{ABC}} = \frac{1}{2}AB \cdot BC = \frac{1}{2} \cdot 1 \cdot 4 = 2\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Thể tích nước đang có trong hồ bơi là \({V_1} = {S_{ABC}} \cdot AA' = 2 \cdot 6 = 12\left( {{{\rm{m}}^3}} \right)\).
Lại có \({S_{ADEF}} = \frac{{\left( {AD + EF} \right) \cdot DE}}{2} = \frac{{\left( {3 + 1} \right) \cdot 12}}{2} = 24\left( {{{\rm{m}}^2}} \right)\).
Thể tích hồ bơi là \(V = {S_{ADEF}}_{\rm{\;}} \cdot AA' = 24 \cdot 6 = 144\,\left( {{{\rm{m}}^3}} \right)\).
Thể tích nước cần bơm vào là \(0,75V - {V_1} = 0,75 \cdot 144 - 12 = 96\,\,\left( {{{\rm{m}}^3}} \right)\).
Thời gian bơm là \(96:0,25 = 384\) (phút).
Đáp án: 384.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.