Nhân dịp tết Trung thu, xí nghiệp sản xuất bánh muốn sản xuất hai loại bánh: bánh nướng và bánh dẻo. Để sản xuất hai loại bánh này, xí nghiệp cần: đường, bột mì, trứng, mứt bí, lạp xưởng. Xí nghiệp đã nhập về 600 kg bột mì và 240 kg đường, các nguyên liệu khác luôn đáp ứng được số lượng mà xí nghiệp cần. Mỗi chiếc bánh nướng cần 120 g bột mì, 60 g đường. Mỗi chiếc bánh dẻo cần 160 g bột mì và 40 g đường. Theo khảo sát thị trường sản phẩm của xí nghiệp sản xuất luôn được tiêu thụ hết. Mỗi chiếc bánh nướng lãi 8000 đồng, mỗi chiếc bánh dẻo lãi 6000 đồng. Để đáp ứng nhu cầu thị trường; đảm bảo lượng bột mì, đường không vượt quá số lượng mà xí nghiệp đã chuẩn bị và vẫn thu được lợi nhuận cao nhất thì xí nghiệp phải sản xuất m chiếc bánh nướng và n chiếc bánh dẻo, với \(m,n\) là các số tự nhiên. Tính giá trị \(\frac{{m + n}}{6}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: 750
Gọi \(x;y\) lần lượt là số lượng chiếc bánh nướng và bánh dẻo mà xí nghiệp sản xuất (\(x,y \ge 0\)).
Theo đề bài ta có hệ bất phương trình \(\left\{ \begin{array}{l}120x + 160y \le 600000\\60x + 40y \le 240000\\x \ge 0\\y \ge 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3x + 4y \le 15000\\3x + 2y \le 12000\\x \ge 0\\y \ge 0\end{array} \right.\) (I).
Tiền lãi thu được là \(F = 8x + 6y\) (nghìn đồng).
Bài toán trở thành tìm giá trị lớn nhất của \(F = 8x + 6y\) trên miền nghiệm của hệ bất phương trình (I).
Miền nghiệm của bất phương trình là miền tứ giác OABC (phần tô màu) như hình vẽ
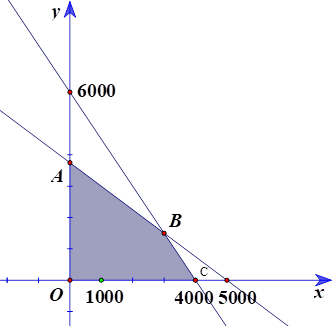
Ta có \(O\left( {0;0} \right),A\left( {0;3750} \right),B\left( {3000;1500} \right),C\left( {4000;0} \right)\).
Có \(F\left( {0;0} \right) = 8.0 + 6.0 = 0\); \(F\left( {0;3750} \right) = 8.0 + 6.3750 = 22500\);
\(F\left( {3000;1500} \right) = 8.3000 + 6.1500 = 33000\); \(F\left( {4000;0} \right) = 8.4000 + 6.0 = 32000\).
Để lợi nhuận cao nhất thì xí nghiệp phải sản xuất 3000 bánh nướng và 1500 bánh dẻo.
Suy ra \(m = 3000;n = 1500\). Do đó \(\frac{{m + n}}{6} = \frac{{3000 + 1500}}{6} = 750\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Trả lời: 212
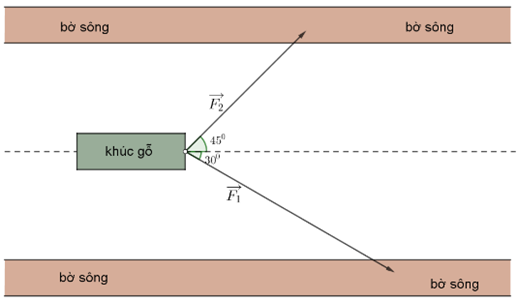
Gọi M là điểm đầu, \(A,B\) là điểm cuối của các vectơ lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \).
Dựng hình bình hành \(MACB\).
Gọi \(\overrightarrow {{F_{12}}} \) là hợp lực của hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \).
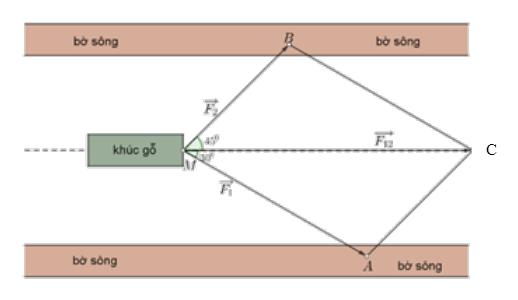
Ta có \(\widehat {MCA} = \widehat {BMC} = 45^\circ ,\widehat {MCB} = \widehat {AMC} = 30^\circ \), \(\widehat {MAC} = 180^\circ - \widehat {AMC} - \widehat {MCA} = 105^\circ \),
\(\widehat {MBC} = \widehat {MAC} = 105^\circ \).
Áp dụng định lí sin trong \(\Delta MAC\):
\(\frac{{MC}}{{\sin \widehat {MAC}}} = \frac{{MA}}{{\sin \widehat {MCA}}}\)\( \Leftrightarrow \frac{{MC}}{{\sin 105^\circ }} = \frac{{300}}{{\sin 45^\circ }}\)\( \Leftrightarrow MC = 150\left( {1 + \sqrt 3 } \right)\).
Áp dụng định lí sin trong \(\Delta MBC\):
\(\frac{{MC}}{{\sin \widehat {MBC}}} = \frac{{MB}}{{\sin \widehat {MCB}}}\)\( \Leftrightarrow \frac{{150\left( {1 + \sqrt 3 } \right)}}{{\sin 105^\circ }} = \frac{{MB}}{{\sin 30^\circ }}\)\( \Leftrightarrow MB = 150\sqrt 2 \).
Vậy người thứ hai cần dùng lực \(150\sqrt 2 \approx 212\) N.
Câu 2
A. \(\overrightarrow {AE} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \).
B. \(\overrightarrow {AE} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
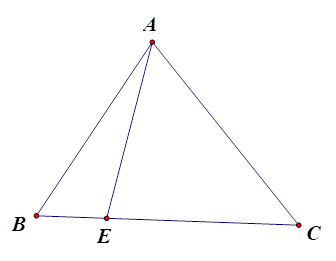
Ta có \(\overrightarrow {AE} = \overrightarrow {AB} + \overrightarrow {BE} \)\( = \overrightarrow {AB} + \frac{1}{4}\overrightarrow {BC} \)\( = \overrightarrow {AB} + \frac{1}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)\( = \overrightarrow {AB} - \frac{1}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \)\( = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} .\)
Câu 3
A. \(\overrightarrow {OB} = \overrightarrow {DO} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 \).
B. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\sin \alpha \) và \(\cot \alpha \) cùng dấu.
B. Tích \(\sin \alpha .\cot \alpha \) mang dấu âm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập