Một chiếc khay đựng đầy nước có dạng hình hộp chữ nhật với các kích thước: chiều dài \(20\) cm, chiều rộng \(10\) cm, chiều cao \(8\) cm (Hình a). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài \(n\,\,\left( {{\rm{cm}}} \right)\), miệng khay là hình vuông lớn có đường chéo dài \(2n\left( {{\rm{cm}}} \right)\) (Hình b). Sau khi đổ, mực nước ở khay thứ hai cao bằng \(\frac{2}{5}\) chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi \(\frac{1}{4}\) so với ban đầu. Thể tích của chiếc khay thứ hai theo đơn vị centimét khối có kết quả chính xác đến hàng đơn vị là \(a\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\), hỏi tổng các chữ số của số \(a\) bằng bao nhiêu?
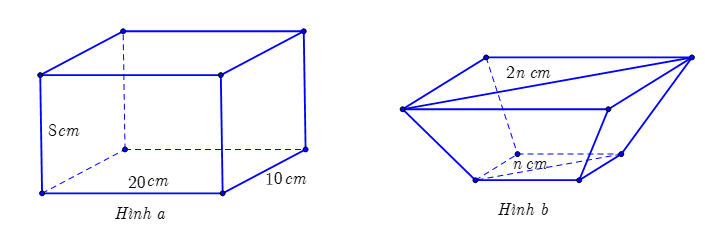
Một chiếc khay đựng đầy nước có dạng hình hộp chữ nhật với các kích thước: chiều dài \(20\) cm, chiều rộng \(10\) cm, chiều cao \(8\) cm (Hình a). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài \(n\,\,\left( {{\rm{cm}}} \right)\), miệng khay là hình vuông lớn có đường chéo dài \(2n\left( {{\rm{cm}}} \right)\) (Hình b). Sau khi đổ, mực nước ở khay thứ hai cao bằng \(\frac{2}{5}\) chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi \(\frac{1}{4}\) so với ban đầu. Thể tích của chiếc khay thứ hai theo đơn vị centimét khối có kết quả chính xác đến hàng đơn vị là \(a\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\), hỏi tổng các chữ số của số \(a\) bằng bao nhiêu?

Câu hỏi trong đề: Đề ôn luyện Toán Chương 5. Hình học không gian (đề số 2) !!
Quảng cáo
Trả lời:
Cách 1:
Vì khay đựng đầy nước có dạng hình hộp chữ nhật với kích thước: chiều dài 20 cm, chiều rộng 10 cm, chiều cao 8 cm, nên ta có thể tích nước trong khay thứ nhất trước khi đổ ra là:
\(20 \cdot 10 \cdot 8 = 1600\) (cm3).
Sau khi đổ nước sang khay thứ hai, ta thấy rằng lượng nước trong khay thứ nhất giảm đi \(\frac{1}{4}\) so với ban đầu, cho nên lượng nước có ở trong khay thứ 2 bằng \(\frac{1}{4}\) lượng nước ban đầu có ở trong khay thứ nhất. Như vậy, thể tích nước có trong khay thứ hai là \(\frac{1}{4} \cdot 1600 = 400\) (cm3).
Gọi chiều cao của khay thứ hai là h (cm).
Giả sử khay thứ hai có hình dạng chóp cụt tứ giác đều \(ABCD.A'B'C'D'\)như hình vẽ sau:
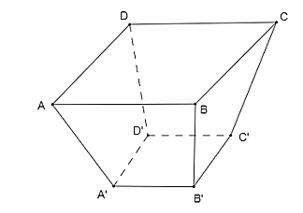
Dễ dàng chứng minh được \(ACC'A'\) là hình thang cân. Lấy \(MN\) song song với \[AC;H,K\]lần lượt là hình chiếu của \(A',C'\) trên \(AC;P,Q\) lần lượt là giao điểm của \(A'H\) và \(MN\), \(C'K\) và \(MN\) như hình vẽ sau:
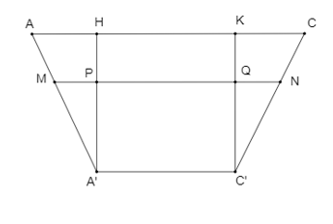
Theo giả thiết mực nước (ngang với \(MN\)) trong khay thứ hai cao bằng \(\frac{2}{5}\) chiều cao của khay đó, nên ta có thể coi \(C'Q\) chính là chiều cao nước trong khay.
Dễ thấy \(A'H = C'K = h\).
Suy ra \(C'Q = \frac{2}{5}h\), có nghĩa là chiều cao nước trong khay thứ hai là \(\frac{2}{5}h\).
Dễ dàng chứng minh được \(HKC'A'\)là hình chữ nhật.
Từ đó ta có \(A'C' = HK = n\), \(AH = CK = \frac{{AC - HK}}{2} = \frac{{2n - n}}{2} = \frac{n}{2}\).
Tam giác \(A'AH\) có \(MP{\rm{//}}AH\) nên theo hệ quả định lí Thales ta có: \(\frac{{MP}}{{AH}} = \frac{{A'P}}{{A'H}} = \frac{2}{5}\)
\( \Rightarrow MP = \frac{2}{5}AH = \frac{2}{5} \cdot \frac{n}{2} = \frac{n}{5}\).
Tương tự tam giác \(C'CK\) có \(QN{\rm{//}}CK\) nên ta cũng có \(QN = \frac{n}{5}\).
Do đó \(MN = MP + PQ + QN = \frac{n}{5} + n + \frac{n}{5} = \frac{{7n}}{5}\).
Theo giả thiết ta có thể tích nước trong khay thứ hai bằng thể tích khối chóp cụt tứ giác đều với đáy lớn (hình vuông) nhận \(MN\) làm đường chéo có diện tích \({S'_1}\) và đáy nhỏ (hình vuông) nhận \(A'C'\) làm đường chéo có diện tích \({S'_2}\) , chiều cao bằng \(h' = \frac{2}{5}h\).
Ta có \[{S'_1} = \frac{{M{N^2}}}{2} = \frac{{{{\left( {\frac{{7n}}{5}} \right)}^2}}}{2} = \frac{{49{n^2}}}{{50}};\,\,{S'_1} = \frac{{A'{{C'}^2}}}{2} = \frac{{{n^2}}}{2}\].
\[ \Rightarrow V' = \frac{1}{3} \cdot \frac{2}{5}h \cdot \left( {\frac{{49{n^2}}}{{50}} + \sqrt {\frac{{49{n^2}}}{{50}} \cdot \frac{{{n^2}}}{2}} + \frac{{{n^2}}}{2}} \right) = \frac{{109}}{{375}}{n^2}h = 400\]\[ \Rightarrow {n^2}h = \frac{{150000}}{{109}}\].
Mặt khác, thể tích khay thứ hai bằng thể tích khối chóp cụt tứ giác đều với đáy lớn (hình vuông) nhận \(AC\) là đường chéo có diện tích \({S_1}\) và đáy nhỏ (hình vuông) nhận \(A'C'\) làm đường chéo có diện tích \({S_2}\), chiều cao bằng \(h\).
\[{S_1} = \frac{{A{C^2}}}{2} = 2{n^2};{S_2} = \frac{{A'{{C'}^2}}}{2} = \frac{{{n^2}}}{2}\]
\[ \Rightarrow V = \frac{1}{3}h \cdot \left( {2{n^2} + \sqrt {2{n^2} \cdot \frac{{{n^2}}}{2}} + \frac{{{n^2}}}{2}} \right) = \frac{7}{6}{n^2}h = \frac{7}{6} \cdot \frac{{150000}}{{109}} \approx 1606\] (cm3).
Vậy tổng các chữ số của số \(a = 1606\) bằng \(13\).
Cách 2:
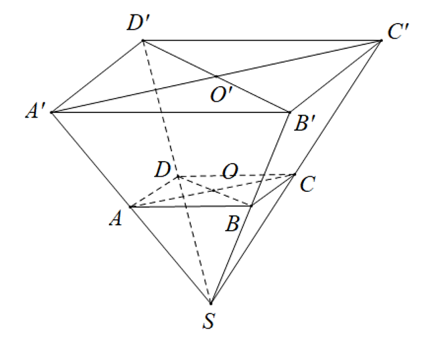
Thể tích nước có trong khay thứ hai là \(V = \frac{1}{4} \cdot 20 \cdot 10 \cdot 8 = 400\) (cm3).
Gọi \(S\) là điểm đồng quy của các cạnh bên của hình chóp cụt.
Dễ dàng chứng minh được \(SO = \frac{1}{2}SO'\).
\( \Rightarrow \) chiều cao của nước trong khay thứ hai là: \(\frac{2}{5} \cdot \frac{1}{2} \cdot SO' = \frac{1}{5}SO'\).
\( \Rightarrow \)khoảng cách từ mặt nước trong khay thứ hai đến \(S\) là: \(\left( {\frac{1}{5} + \frac{1}{2}} \right) \cdot SO' = \frac{7}{{10}}SO'\).
Mà tỉ số thể tích bằng lập phương tỉ số đồng dạng
\( \Rightarrow V = 400 = {\left( {\frac{7}{{10}}} \right)^3} \cdot {V_{S.A'B'C'D'}} - {\left( {\frac{1}{2}} \right)^3} \cdot {V_{S.A'B'C'D'}} \Rightarrow {V_{S.A'B'C'D'}} \approx 1834,86\) (cm3).
\( \Rightarrow \)Thể tích của chiếc khay thứ hai bằng \(\frac{7}{8}{V_{S.A'B'C'D'}} \approx 1606\).
Vậy tổng các chữ số của số \(a = 1606\) bằng \(13\).
Đáp án: 13.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
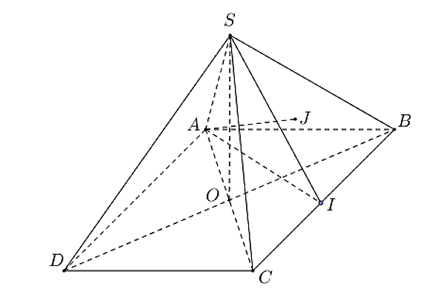
Theo tính chất của hình chóp đều, ta có \(SO \bot \left( {ABCD} \right)\).
Thể tích khối chóp \(S.ABCD\) là \({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot {2^2} \cdot 2 = \frac{8}{3} \Rightarrow {V_{S.ABC}} = \frac{1}{2} \cdot {V_{S.ABCD}} = \frac{4}{3}.\)
Gọi \(I\) là trung điểm của \(CB\), tam giác \(SBC\) có \(SC = SB = \sqrt {S{O^2} + O{B^2}} = \sqrt {{2^2} + {{\left( {\sqrt 2 } \right)}^2}} = \sqrt 6 \) và \(SI = \sqrt {S{O^2} + O{I^2}} = \sqrt {{2^2} + {1^2}} = \sqrt 5 \) nên có diện tích bằng \({S_{\Delta SBC}} = \frac{1}{2} \cdot SI \cdot BC = \frac{1}{2} \cdot \sqrt 5 \cdot 2 = \sqrt 5 \).
Gọi \(J\) là hình chiếu của \(A\) lên mặt phẳng \(\left( {SBC} \right)\), gọi \(\varphi \) là góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBC} \right)\) thì \(\sin \varphi = \sin \widehat {ASJ} = \frac{{AJ}}{{SA}} = \frac{{d\left( {A,\left( {SBC} \right)} \right)}}{{SA}}.\)
Mà \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{3{V_{S.ABC}}}}{{{S_{\Delta SBC}}}} = \frac{4}{{\sqrt 5 }}\). Vậy \(\sin \varphi = \frac{{d\left( {A,\left( {SBC} \right)} \right)}}{{SA}} = \frac{{2\sqrt {30} }}{{15}} \approx 0,73\).
Đáp án: 0,73.
Lời giải
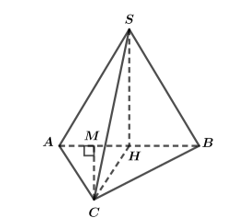
a) Đúng. \(\Delta SAB\) đều, \(H\) là trung điểm \(AB\) \( \Rightarrow SH \bot AB\).
Ta có
b) Đúng. Mặt khác, ta có \(SH \subset \left( {SHC} \right) \Rightarrow \left( {SHC} \right) \bot \left( {ABC} \right)\).
c) Sai. \(\Delta SAB\) đều cạnh bằng \(2a\)\( \Rightarrow SH = a\sqrt 3 \).
\(\Delta ABC\) vuông tại \(C\) \( \Rightarrow CB = \sqrt {A{B^2} - A{C^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {a\sqrt 3 } \right)}^2}} = a\) (Pythagore).
Vậy \({V_{S.ABC}} = \frac{1}{3} \cdot {S_{ABC}} \cdot SH = \frac{1}{3} \cdot \frac{{AC \cdot CB}}{2} \cdot SH = \frac{1}{3} \cdot \frac{{a\sqrt 3 .a}}{2} \cdot a\sqrt 3 = \frac{1}{2}{a^3}\).
d) Sai. Kẻ \(CM \bot AB\) tại M.
Xét \(\Delta ABC\) vuông tại \(C\) có: \(CM \cdot AB = AC \cdot CB \Rightarrow CM = \frac{{AC \cdot CB}}{{AB}} = \frac{{\sqrt 3 }}{2}a\).
Ta có
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
