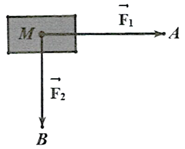
Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\). Cường độ hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \)lần lượt là 300N và 400N, \(\widehat {AMB} = 90^\circ \). Tìm cường độ của lực tác động lên vật?
Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\). Cường độ hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \)lần lượt là 300N và 400N, \(\widehat {AMB} = 90^\circ \). Tìm cường độ của lực tác động lên vật?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: 500
Ta có tổng lực tác dụng lên vật: \({\vec F_1} + {\vec F_2} = \overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MC} \) (Với \(C\) là điểm sao cho \(AMBC\) là hình bình)
Khi đó cường độ lực tác dụng lên vật: \(\left| {{{\vec F}_1} + {{\vec F}_2}} \right| = |\overrightarrow {MC} | = MC\)
Ta có: \(MA = |\overrightarrow {MA} | = \left| {{{\vec F}_1}} \right| = 400\;N\), \(MB = |\overrightarrow {MB} | = \left| {{{\vec F}_2}} \right| = 300\;N\)
Mặt khác, do \(\widehat {AMB} = 90^\circ \) nên \(AMBC\) là hình chữ nhật.
Khi đó: \(MC = \sqrt {M{A^2} + M{B^2}} = \sqrt {{{400}^2} + {{300}^2}} = 500{\rm{(N)}}\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) S, b) Đ, c) Đ, d) S
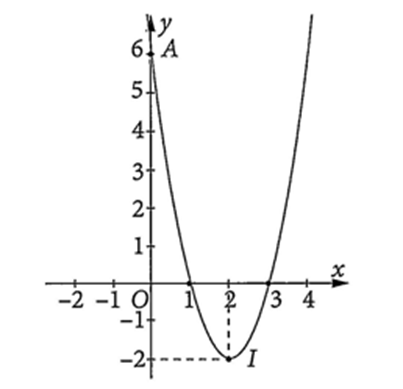
a) Trục đối xứng của đồ thị là đường thẳng \(x = 2\).
b) Đỉnh \(I\) của đồ thị hàm số có tọa độ là \((2; - 2)\).
c) Đồ thị hàm số đi qua điểm \(A(0;6)\).
b) Hàm số bậc hai có dạng \(y = a{x^2} + bx + c(a \ne 0)\). Đồ thị hàm số đi qua điểm \(A(0;6)\) nên \(a \cdot {0^2} + b \cdot 0 + c = 6 \Rightarrow c = 6\).
Mặt khác, đồ thị có toạ độ đỉnh là \(I(2; - 2)\) nên ta có:
\(\begin{array}{*{20}{c}}{\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\a \cdot {2^2} + b \cdot 2 + 6 = - 2\end{array} \right.}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}4a + b = 0\\4a + 2b = - 8\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}a = 2\\b = - 8\end{array}\end{array}{\rm{. }}} \right.} \right.\)
Vậy hàm số đã cho là \(y = 2{x^2} - 8x + 6\).
Câu 2
A. \(\overrightarrow {AN} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \).
B. \(\overrightarrow {AN} = \frac{1}{6}\overrightarrow {AB} - \frac{5}{6}\overrightarrow {AC} \).
C. \(\overrightarrow {AN} = \frac{1}{6}\overrightarrow {AB} + \frac{5}{6}\overrightarrow {AC} \).
D. \(\overrightarrow {AN} = - \frac{1}{6}\overrightarrow {AB} + \frac{5}{6}\overrightarrow {AC} \).
Lời giải
Đáp án đúng là: C
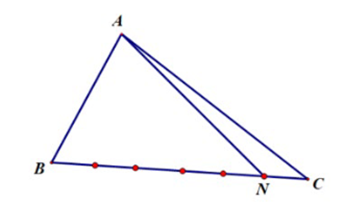
Ta có \(N\) thuộc cạnh \(BC\) sao cho \(MB = \frac{5}{6}BC \Rightarrow \overrightarrow {CN} = \frac{1}{6}\overrightarrow {CB} \).
Ta có \(\overrightarrow {AN} = \overrightarrow {AC} + \overrightarrow {CN} = \overrightarrow {AC} + \frac{1}{6}\overrightarrow {CB} \) \( = \overrightarrow {AC} + \frac{1}{6}\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \frac{1}{6}\overrightarrow {AB} + \frac{5}{6}\overrightarrow {AC} \).
Câu 3
A. \(\overrightarrow {AM} \).
B. \(\overrightarrow {MN} \).
C. \(\overrightarrow {PB} \).
D. \(\overrightarrow {AP} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\alpha = 30^\circ \).
B. \(\alpha = 45^\circ \).
C. \(\alpha = 60^\circ \).
D. \(\alpha = 120^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{a}{2}\).
B. \(2a\).
C. \(a\sqrt 2 \).
D. \(a\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập