Các thí sinh tham dự một cuộc thi hoa khôi phải trải qua ba vòng thi: vòng sơ khảo, vòng bán kết và vòng chung kết. Biết rằng, ban tổ chức sẽ chọn ra \(50{\rm{\% }}\) thí sinh đã đăng kí để vào vòng sơ khảo. Khi kết thúc vòng sơ khảo, ban tổ chức sẽ chọn ra \(30{\rm{\% }}\) thí sinh của vòng sơ khảo để vào vòng bán kết. Khi kết thúc vòng bán kết, ban tổ chức sẽ chọn ra \(20{\rm{\% }}\) thí sinh của vòng bán kết để vào vòng chung kết. Chọn ngẫu nhiên 1 thí sinh đăng kí tham dự cuộc thi hoa khôi.
a) Xác suất để thí sinh được chọn lọt vào vòng sơ khảo là \(0,5\).
b) Xác suất để thí sinh được chọn lọt vào vòng bán kết là \(0,3\).
c) Xác suất thí sinh được chọn lọt vào vòng chung kết là \(0,03\).
d) Biết rằng thí sinh được chọn không lọt vào vòng chung kết, xác suất thí sinh đó lọt vào vòng sơ khảo nhỏ hơn \(0,49\).
Quảng cáo
Trả lời:
Gọi \(A,B,C\) lần lượt là biến cố thí sinh được chọn lọt vào vòng sơ khảo, vòng bán kết và vòng chung kết.
a) Đúng. Vì có \(50{\rm{\% }}\) thí \({\rm{sinh}}\) lọt vào vòng sơ khảo nên \(P\left( A \right) = 0,5\).
b) Sai. Xác suất để thí sinh lọt vào vòng bán kết là
\({\rm{\;}}P\left( B \right) = P\left( {AB} \right) = P\left( {B\mid A} \right)P\left( A \right) = 0,3 \cdot 0,5 = 0,15\).
c) Đúng. Xác suất để thí sinh lọt vào vòng chung kết là
\(P\left( C \right) = P\left( {ABC} \right) = P\left( {C\mid AB} \right)P\left( {AB} \right) = 0,2 \cdot 0,15 = 0,03\).
d) Sai. Ta có \(P\left( {\overline C \mid A} \right) = 1 - P\left( {C\mid A} \right) = 1 - \frac{{P\left( C \right)}}{{P\left( A \right)}} = 0,94\).
Do đó, \[P\left( {A\mid \overline C } \right) = \frac{{P\left( {\overline C \mid A} \right)P\left( A \right)}}{{P\left( {\overline C } \right)}} = \frac{{0,94 \cdot 0,5}}{{1 - 0,03}} = \frac{{47}}{{97}} \approx 0,485 < 0,49\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(A\) là biến cố bệnh nhân được điều trị bằng phác đồ \(A\) thì \(\overline A \) là biến cố bệnh nhân được điều trị bằng phác đồ \(B\). Ta có \(P\left( A \right) = P\left( {\overline A } \right) = 0,5.\)
Gọi \(X\) là biến cố bệnh nhân được chữa khỏi bệnh. Ta có \(P\left( {X|A} \right) = 0,6;\,\,P\left( {X|\overline A } \right) = 0,7.\)
Gọi \(Y\) là biến cố bệnh nhân bị tác dụng phụ nghiêm trọng. Ta có \(P\left( {Y|A} \right) = 0,05;\,\,P\left( {Y|\overline A } \right) = 0,1.\)
a) Sai. Xác suất bệnh nhân điều trị bằng phác đồ \(A\) và được chữa khỏi bệnh là:
\(P\left( {AX} \right) = P\left( A \right) \cdot P\left( {X|A} \right) = 0,5 \cdot 0,6 = 0,3.\)
b) Đúng. Xác suất để bệnh nhân bị tác dụng phụ nghiêm trọng là:
\(P\left( Y \right) = P\left( A \right) \cdot P\left( {Y|A} \right) + P\left( {\overline A } \right) \cdot P\left( {Y|\overline A } \right) = 0,5 \cdot 0,05 + 0,5 \cdot 0,1 = 0,075.\)
c) Đúng. Nếu biết bệnh nhân này gặp tác dụng phụ nghiêm trọng thì xác suất bệnh nhân được điều trị bằng phác đồ \(B\) là:
\(P\left( {\overline A |Y} \right) = \frac{{P\left( {\overline A Y} \right)}}{{P\left( Y \right)}} = \frac{{P\left( {\overline A } \right) \cdot P\left( {Y|\overline A } \right)}}{{P\left( Y \right)}} = \frac{{0,5 \cdot 0,1}}{{0,075}} \approx 0,67 > 0,65.\)
d) Đúng. Ta có \(P\left( X \right) = P\left( A \right) \cdot P\left( {X|A} \right) + P\left( {\overline A } \right) \cdot P\left( {X|\overline A } \right) = 0,5 \cdot 0,6 + 0,5 \cdot 0,7 = 0,65.\)
Do biến cố “bệnh nhân được chữa khỏi bệnh” và biến cố “bệnh nhân không bị tác dụng phụ nghiêm trọng” là độc lập với nhau. Nên xác suất bệnh nhân khỏi bệnh và không bị tác dụng phụ nghiêm trọng là:
\[P\left( {X\overline Y } \right) = P\left( {X\overline Y |A} \right)P\left( A \right) + P\left( {X\overline Y |\overline A } \right)P\left( {\overline A } \right) = \left[ {0,6 \cdot \left( {1 - 5\% } \right)} \right]0,5 + \left[ {0,7 \cdot \left( {1 - 10\% } \right)} \right]0,5 = 0,6\].
Lời giải
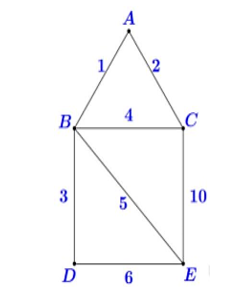
Đồ thị trên chỉ có hai đỉnh bậc lẻ là C và E nên ta có thể tìm được một đường đi Euler từ C đến E (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ C đến E là CABDEBCE và tổng độ dài của nó là
\(2 + 1 + 3 + 6 + 5 + 4 + 10 = 31\,\,{\rm{(km)}}\).
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ E đến C.
Đường đi ngắn nhất từ \(E\) đến \(C\) là \(EBAC\) và có độ dài là \(5 + 1 + 2 = 8\,{\rm{(km)}}\).
Vậy tổng quãng đường đưa thư có thể đi ngắn nhất là \(31 + 8 = 39\,({\rm{km}})\).
Đáp án: 39.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.