Trong chuyện cổ tích “Cây tre trăm đốt”, khi không vác được cây tre dài đến \[100\] đốt về nhà, anh Khoai ngồi khóc. Bụt hiện lên, bày cho anh một cách hay: “Con hãy đọc câu thần chú “khắc xuất, khắc xuất” thì cây tre sẽ phân tách ra nhiều thanh nhỏ để con có thể mang được về nhà. Biết rằng sau mỗi câu thần chú như thế thì cây tre \[100\] đốt được tách ra một cách ngẫu nhiên thành các đoạn ngắn có chiều dài \[2\] đốt và \[5\] đốt (có thể chỉ có một loại). Tính xác suất để số đoạn \[2\] đốt nhiều hơn số đoạn \[5\] đốt đúng \[1\] đơn vị (làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số đoạn tre có chiều dài \[2\] đốt và \[5\] đốt mà cây tre có thể phân tách được thành lần lượt là \(x\) và \(y\)\(\left( {x,y \in \mathbb{N}} \right)\).
Khi đó, ta có: \(2x + 5y = 100 \Leftrightarrow y = \frac{{100 - 2x}}{5} = 20 - 2 \cdot \frac{x}{5}\).
Do \(y \in \mathbb{N}\) nên \(\left\{ {\begin{array}{*{20}{c}}{20 - 2 \cdot \frac{x}{5} \ge 0}\\{x\,\, \vdots \,\,5}\end{array}} \right. \Rightarrow x \in \left\{ {0;5;...;50} \right\}\).
Do ứng với mỗi giá trị \(x\) ta có một giá trị \(y\) tương ứng nên ta có \(11\) cách chia cây tre thành \(2\) loại có chiều dài \[2\] đốt và \[5\] đốt.
Gọi \(\Omega \) là không gian mẫu \[ \Rightarrow n\left( \Omega \right) = 11\].
Gọi biến cố \(A\): “Cây tre được chia thành đoạn có chiều dài \[2\] đốt và \[5\] đốt sao cho số đoạn \[2\] đốt nhiều hơn số đoạn \[5\] đốt đúng \[1\] đơn vị”.
Để số đoạn có có chiều dài \[2\] đốt nhiều hơn số đoạn có chiều dài \[5\] đốt đúng một đơn vị thì \(x - y = 1\). Khi đó, ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{2x + 5y = 100}\\{x - y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 15}\\{y = 14}\end{array}} \right. \Rightarrow n\left( A \right) = 1\).
Khi đó, \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{{11}} \approx 0,09\].
Đáp án: 0,09.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(A\) là biến cố bệnh nhân được điều trị bằng phác đồ \(A\) thì \(\overline A \) là biến cố bệnh nhân được điều trị bằng phác đồ \(B\). Ta có \(P\left( A \right) = P\left( {\overline A } \right) = 0,5.\)
Gọi \(X\) là biến cố bệnh nhân được chữa khỏi bệnh. Ta có \(P\left( {X|A} \right) = 0,6;\,\,P\left( {X|\overline A } \right) = 0,7.\)
Gọi \(Y\) là biến cố bệnh nhân bị tác dụng phụ nghiêm trọng. Ta có \(P\left( {Y|A} \right) = 0,05;\,\,P\left( {Y|\overline A } \right) = 0,1.\)
a) Sai. Xác suất bệnh nhân điều trị bằng phác đồ \(A\) và được chữa khỏi bệnh là:
\(P\left( {AX} \right) = P\left( A \right) \cdot P\left( {X|A} \right) = 0,5 \cdot 0,6 = 0,3.\)
b) Đúng. Xác suất để bệnh nhân bị tác dụng phụ nghiêm trọng là:
\(P\left( Y \right) = P\left( A \right) \cdot P\left( {Y|A} \right) + P\left( {\overline A } \right) \cdot P\left( {Y|\overline A } \right) = 0,5 \cdot 0,05 + 0,5 \cdot 0,1 = 0,075.\)
c) Đúng. Nếu biết bệnh nhân này gặp tác dụng phụ nghiêm trọng thì xác suất bệnh nhân được điều trị bằng phác đồ \(B\) là:
\(P\left( {\overline A |Y} \right) = \frac{{P\left( {\overline A Y} \right)}}{{P\left( Y \right)}} = \frac{{P\left( {\overline A } \right) \cdot P\left( {Y|\overline A } \right)}}{{P\left( Y \right)}} = \frac{{0,5 \cdot 0,1}}{{0,075}} \approx 0,67 > 0,65.\)
d) Đúng. Ta có \(P\left( X \right) = P\left( A \right) \cdot P\left( {X|A} \right) + P\left( {\overline A } \right) \cdot P\left( {X|\overline A } \right) = 0,5 \cdot 0,6 + 0,5 \cdot 0,7 = 0,65.\)
Do biến cố “bệnh nhân được chữa khỏi bệnh” và biến cố “bệnh nhân không bị tác dụng phụ nghiêm trọng” là độc lập với nhau. Nên xác suất bệnh nhân khỏi bệnh và không bị tác dụng phụ nghiêm trọng là:
\[P\left( {X\overline Y } \right) = P\left( {X\overline Y |A} \right)P\left( A \right) + P\left( {X\overline Y |\overline A } \right)P\left( {\overline A } \right) = \left[ {0,6 \cdot \left( {1 - 5\% } \right)} \right]0,5 + \left[ {0,7 \cdot \left( {1 - 10\% } \right)} \right]0,5 = 0,6\].
Lời giải
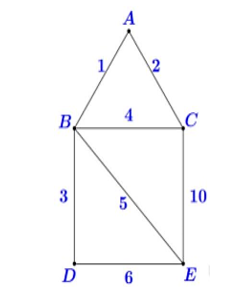
Đồ thị trên chỉ có hai đỉnh bậc lẻ là C và E nên ta có thể tìm được một đường đi Euler từ C đến E (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ C đến E là CABDEBCE và tổng độ dài của nó là
\(2 + 1 + 3 + 6 + 5 + 4 + 10 = 31\,\,{\rm{(km)}}\).
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ E đến C.
Đường đi ngắn nhất từ \(E\) đến \(C\) là \(EBAC\) và có độ dài là \(5 + 1 + 2 = 8\,{\rm{(km)}}\).
Vậy tổng quãng đường đưa thư có thể đi ngắn nhất là \(31 + 8 = 39\,({\rm{km}})\).
Đáp án: 39.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(7,91\).
B. \(8,38\).
C. \(8,37\).
D. \(7,95\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{\sqrt {285} }}{3}\).
B. \(\frac{{\sqrt {287} }}{3}\).
C. \(4\sqrt 2 \).
D. \(\sqrt {71} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 30,0 triệu đồng.
B. 42,5 triệu đồng.
C. 56,7 triệu đồng.
D. 53,7 triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập