Công ty X có một kho hàng trung tâm tại điểm A và cần giao hàng đến 3 điểm giao hàng khác nhau B, C, D trong thành phố, sau khi giao hàng xong thì xe quay về điểm A. Biết rằng khoảng cách giữa các điểm giao hàng cho bởi bảng sau (đơn vị tính km).
|
Điểm đến Điểm đi |
A |
B |
C |
D |
|
A |
0 |
9 |
11 |
14 |
|
B |
9 |
0 |
7 |
8 |
|
C |
11 |
7 |
0 |
5 |
|
D |
14 |
8 |
5 |
0 |
Thời gian giao hàng tại mỗi điểm giao hàng 30 phút/điểm. Tốc độ trung bình của xe vận chuyển hàng là 40km/h. Tính tổng thời gian ít nhất để hoàn thành việc giao hàng nói trên (đơn vị đo: phút, làm tròn đến hàng đơn vị).
Quảng cáo
Trả lời:
Từ giả thiết của đề bài, ta có đồ thị sau:
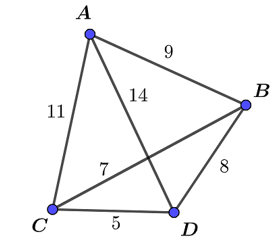
Ta thấy đây là một đơn đồ thị có 4 đỉnh, mỗi đỉnh đều có bậc là 3 không nhỏ hơn \(\frac{4}{2} = 2\) nên theo định lí Dirac thì đồ thị này có một chu trình Hamilton.
Ta xét tất cả các trường hợp sau:
ABCDA: \(9 + 7 + 5 + 14 = 35\).
ABDCA: \(9 + 8 + 5 + 11 = 33\).
ACBDA: \(11 + 7 + 8 + 14 = 40\).
ACDBA: \(11 + 5 + 8 + 9 = 33\).
ADCBA: \(14 + 5 + 7 + 9 = 35\).
ADBCA: \(14 + 8 + 7 + 11 = 40\).
Vậy con đường ngắn nhất đi từ A qua các kho B, C, D và trở về A ngắn nhất là ABDCA hoặc ACDBA, với quãng đường dài \(33\,\,{\rm{km}}\).
Vậy thời gian tối thiểu là: \(\frac{{33}}{{40}} \cdot 60 + 3 \cdot 30 = 139,5\) (phút).
Kết quả làm tròn đến hàng đơn vị là \(140\).
Đáp án: 140.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có không gian mẫu là \(n\left( \Omega \right) = 10!\).
Gọi A là biến cố: “Không có học sinh nào cùng lớp ngồi đối diện nhau”;
\(\overline A \) là biến cố “Có ít nhất 2 học sinh cùng lớp ngồi đối diện nhau”;
\({A_1}\) là biến cố: “Học sinh lớp 12A ngồi đối diện nhau”;
\({A_2}\) là biến cố: “Học sinh lớp 12B ngồi đối diện nhau”.
Khi đó \(n\left( {\overline A } \right) = n\left( {{A_1}} \right) + n\left( {{A_2}} \right) - n\left( {{A_1} \cap {A_2}} \right)\).
- Đếm \(n\left( {{A_1}} \right)\): Trước hết cặp ghế cho 2 học sinh 12A ngồi có 5 cách, đổi chỗ 2 bạn này có \(2!\) cách xếp; xếp 8 học sinh còn lại có \(8!\) cách. Do đó \(n\left( {{A_1}} \right) = 5 \cdot 2!\, \cdot 8!\).
- Đếm \(n\left( {{A_2}} \right)\): Chọn cặp ghế chứa 2 học sinh lớp 12B có 5 cách, chọn 2 học sinh lớp 12B xếp vào cặp ghế này có \(A_3^2\) cách; xếp 8 học sinh còn lại có \(8!\) cách. Do đó \(n\left( {{A_2}} \right) = 5 \cdot A_3^2 \cdot 8!\).
- Đếm \(n\left( {{A_1} \cap {A_2}} \right)\): Chọn 2 cặp ghế trong 5 cặp ghế có \(C_5^2\) cách; trong 2 cặp này chọn 1 cặp cho 2 học sinh lớp 12A có 2 cách, đổi chỗ 2 học sinh này có \(2!\) cách; chọn 2 học sinh lớp 12B xếp vào cặp ghế còn lại có \(A_3^2\) cách; xếp 6 học sinh còn lại có \(6!\) cách.
Do đó \(n\left( {{A_1} \cap {A_2}} \right) = C_5^2 \cdot 2 \cdot 2! \cdot A_3^2 \cdot 6!\).
Suy ra \(n\left( {\overline A } \right) = n\left( {{A_1}} \right) + n\left( {{A_2}} \right) - n\left( {{A_1} \cap {A_2}} \right) = 1\,440\,000\).
Từ đó \(P\left( {\overline A } \right) = \frac{{25}}{{63}} \Rightarrow P\left( A \right) = \frac{{38}}{{63}} \approx 0,6\).
Đáp án: 0,6.
Lời giải
Ta có \(x + 120 + y + 70 + 60 = 400\)\( \Leftrightarrow x + y = 150\).
Trường hợp 1: \[x > 100 \Rightarrow 0 < y < 50\].
Ta có \[{Q_1} \in \left[ {0;20} \right)\] nên \[{Q_1} = 0 + \frac{{\frac{{400}}{4}}}{x}.\left( {20 - 0} \right) = \frac{{2000}}{x}\].
Ta có \({Q_3}\)\( \in \left[ {60;\,80} \right)\) nên \({Q_3} = 60 + \frac{{\frac{{3 \cdot 400}}{4} - \left( {x + y + 120} \right)}}{{70}} \cdot \left( {80 - 60} \right)\)\( = \frac{{480}}{7}\).
\({\Delta _Q} = \frac{{845}}{{21}}\)\( \Leftrightarrow {Q_3} - {Q_1} = \frac{{845}}{{21}}\)\( \Leftrightarrow \frac{{480}}{7} - \frac{{2000}}{x} = \frac{{845}}{{21}} \Leftrightarrow x = \frac{{1200}}{{17}} < 100\) (không thỏa mãn).
Trường hợp 2: \(0 < x \le 100 \Rightarrow 50 \le y < 150\).
Khi đó, \({Q_1}\)\( \in \left[ {20;\,40} \right)\). Suy ra \({Q_1} = 20 + \frac{{\frac{{400}}{4} - x}}{{120}} \cdot \left( {40 - 20} \right) = 20 + \frac{{100 - x}}{6}\).
Ta có \({Q_3}\)\( \in \left[ {60;\,80} \right)\). Suy ra \({Q_3} = 60 + \frac{{\frac{{3 \cdot 400}}{4} - \left( {x + y + 120} \right)}}{{70}} \cdot \left( {80 - 60} \right)\)\( = \frac{{480}}{7}\).
\({\Delta _Q} = \frac{{845}}{{21}}\)\( \Leftrightarrow {Q_3} - {Q_1} = \frac{{845}}{{21}}\)\( \Leftrightarrow \frac{{480}}{7} - \left( {20 + \frac{{100 - x}}{6}} \right) = \frac{{845}}{{21}}\)\( \Leftrightarrow x = 50\) (thỏa mãn).
Suy ra \(y = 100\).
Vậy ta có mẫu số liệu hoàn thiện như sau:

Thời gian tự học trung bình của 400 học sinh là
\(\frac{{10 \cdot 50 + 30 \cdot 120 + 50 \cdot 100 + 70 \cdot 70 + 90 \cdot 60}}{{400}} = 48,5\).
Đáp án: 48,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.