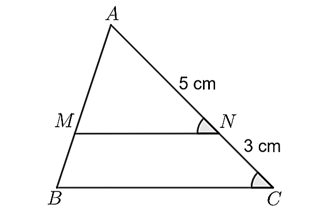
Cho \(\Delta ABC,\) một đường thẳng bất kì song song với \(BC\) cắt hai cạnh \(AB;\;\,AC\) lần lượt tại \(M\) và \(N.\) Khi đó:
B. \(\Delta AMN \sim \Delta ABC.\)
Quảng cáo
Trả lời:
Đáp án đúng là: B
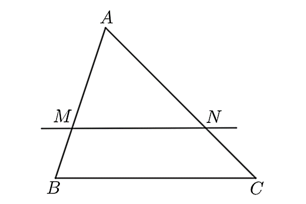
\(\Delta ABC\) có \(MN\;{\rm{//}}\;BC\) nên \(\Delta AMN \sim \Delta ABC.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
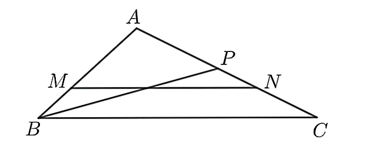
a) Sai.
\(\Delta ABC\) có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\;\,\left( { = \frac{2}{3}} \right)\) nên \(MN\;{\rm{//}}\;BC\) (định lí Thalès đảo).
b) Đúng.
\(\Delta ABC\) có \(MN\;{\rm{//}}\;BC\) nên \(\Delta AMN \sim \Delta ABC.\)
c) Đúng.
\(\Delta APB\) và \(\Delta AMN\) có: \(AP = AM,\;\,AB = AN,\;\,\widehat A\) chung nên \(\Delta APB = \Delta AMN\;\,\left( {{\rm{c}}{\rm{.g}}{\rm{.c}}} \right).\)
Vậy \(\Delta APB = \Delta AMN.\)
d) Sai.
Vì \(\Delta APB = \Delta AMN,\;\,\Delta AMN \sim \Delta ABC\) nên \(\Delta APB \sim \Delta ABC.\)
Lời giải
Đáp án: \(70\)
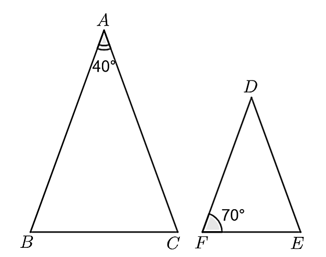
Vì \(\Delta ABC \sim \Delta DEF\) nên \(\widehat D = \widehat A = 40^\circ .\)
\(\Delta DEF\) có: \(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác) nên \(40^\circ + \widehat E + 70^\circ = 180^\circ .\)
Vậy \(\widehat E = 70^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.