II. PHẦN TỰ LUẬN (3 ĐIỂM)

(1,0 điểm) Cho tập hợp \[C = \left[ { - 3;\,8} \right]\] và \[D = \left[ {m - 3;\,8} \right]\].

a) Cho tập hợp \[A = \left( { - \infty ;\, - 3} \right]\] và \[A\backslash C = B\]. Tìm \[B\].

b) Với giá trị nào của m thì \[C \cap D\] là một đoạn thẳng có độ dài bằng 4.

Hướng dẫn giải

Đáp án đúng là: A

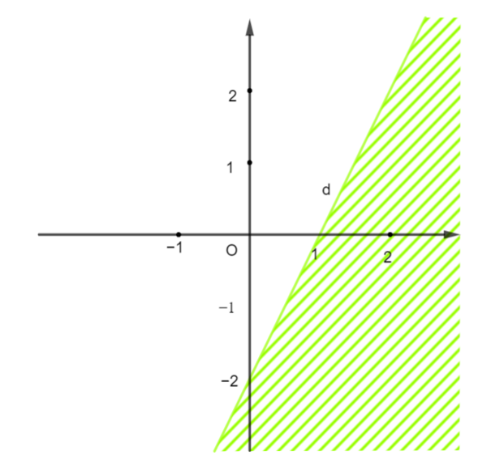
Gọi phương trình đường thẳng \[d\] có dạng: \[y = ax + b\].

Đường thẳng \[d\] đi qua điểm \[\left( {1;\,0} \right)\] và \[\left( {0;\, - 2} \right)\] nên ta có hệ phương trình:

\[\left\{ \begin{array}{l}a + b = 0\\0a + b = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 2\end{array} \right.\]

Vậy \[d\]: \[y = 2x - 2\]hay \[2x--y = 2\]

Lấy điểm \[\left( {0;\,1} \right)\] thuộc miền nghiệm của bất phương trình cần tìm, thay tọa độ điểm \[\left( {0;\,1} \right)\] vào biểu thức \[2x--y = 2\] ta được: \[2.0--1 = - 1 < 2\].

Vậy miền nghiệm được biểu diễn bởi nửa mặt phẳng không bị gạch (kể cả đường thẳng \[d\]) là miền nghiệm của bất phương trình\[2x--y \le 2\].

Hướng dẫn giải

Đáp án đúng là: A

Các tập con của tập \(A\) là: \(\left\{ 1 \right\},\,\left\{ 2 \right\},\,\left\{ 3 \right\},\,\,\left\{ {1;\,\,2} \right\},\,\left\{ {1;\,\,3} \right\},\,\,\left\{ {2;\,\,3} \right\},\,\,\left\{ {1;\,\,2;\,\,3} \right\},\,\,\emptyset \).

Vậy tập không là con của tập \(A\) là: \(\left\{ {12;\,3} \right\}\).