Cho tam giác \(ABC\), điểm \(I\) nằm trong tam giác, các tia \(AI,BI,CI\) cắt các cạnh \(BC,AC,AB\) theo thứ tự ở \(D,E,F\). Qua \(A\) kẻ đường thẳng song song với \(BC\) cắt tia \(CI\) tại \(H\) và cắt tia \(BI\) tại \(K\).
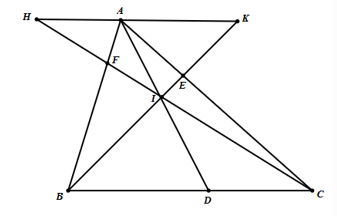
Khi đó:
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng.
Vì \(AK\parallel BD\) nên áp dụng định lí Thalès, ta có: \(\frac{{AI}}{{ID}} = \frac{{AK}}{{BD}}.\) (1)
Vì \(AH\parallel DC\) nên suy ra \(\frac{{AI}}{{ID}} = \frac{{AH}}{{DC}}\) (2)
Từ (1) và (2) suy ra \(\frac{{AK}}{{BD}} = \frac{{AH}}{{DC}}\).
b) Đúng.
Ta có \(\frac{{AF}}{{BF}} = \frac{{AH}}{{BC}}{\rm{ }}\left( {AH\parallel BC} \right)\) và \(\frac{{AE}}{{CE}} = \frac{{AK}}{{BC}}{\rm{ }}\left( {AK\parallel BC} \right)\).
Do đó, \(\frac{{AF}}{{BF}} + \frac{{AE}}{{CE}} = \frac{{AH}}{{BC}} + \frac{{AK}}{{BC}} = \frac{{HK}}{{BC}}.\)
c) Đúng.
Lại có \(\frac{{HK}}{{BC}} = \frac{{HI}}{{IC}}{\rm{ }}\left( {HK\parallel BC} \right)\) và \(\frac{{HI}}{{IC}} = \frac{{AI}}{{ID}}{\rm{ }}\left( {AH\parallel BC} \right)\).
Từ đây suy ra \(\frac{{AF}}{{BF}} + \frac{{AE}}{{CE}} = \frac{{HK}}{{BC}} = \frac{{HI}}{{IC}} = \frac{{AI}}{{ID}}\).
Suy ra \(\frac{{AE}}{{CE}} + \frac{{AF}}{{BF}} = \frac{{AI}}{{ID}}\).
d) Sai.
Từ phần a), ta có: \(\frac{{AK}}{{BD}} = \frac{{AH}}{{DC}}\) suy ra \(\frac{{BD}}{{DC}} = \frac{{AK}}{{AH}}\).
Lại có \(AK\parallel BC\) suy ra \(\frac{{EC}}{{EA}} = \frac{{BC}}{{AK}}\).
Mặt khác \(AH\parallel BC\) nên \(\frac{{FA}}{{FB}} = \frac{{HA}}{{BC}}\).
Từ đây suy ra \(\frac{{BD}}{{DC}} \cdot \frac{{EC}}{{EA}} \cdot \frac{{FA}}{{FB}} = \frac{{AK}}{{AH}} \cdot & \frac{{BC}}{{AK}} \cdot \frac{{HA}}{{BC}} = 1.\)
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
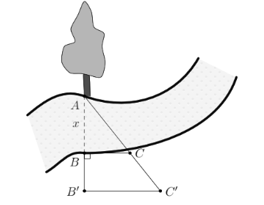
Có \(BC \bot AB',\,B'C' \bot AB'\) nên \(BC\parallel B'C'\).
Do đó, \(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}}\) (Hệ quả của định lí Thalès)
Suy ra \(\frac{{AB}}{{AB + BB'}} = \frac{{BC}}{{B'C'}}\) hay \(\frac{x}{{x + 20}} = \frac{{30}}{{40}}\)
Suy ra \(40x = 30\left( {x + 20} \right)\) nên \(x = 60\,\,\left( {\rm{m}} \right)\).
Câu 2
c) \(\frac{{AB}}{{AD}} = \frac{{ED}}{{CB}}\).
Lời giải
a) Đúng.
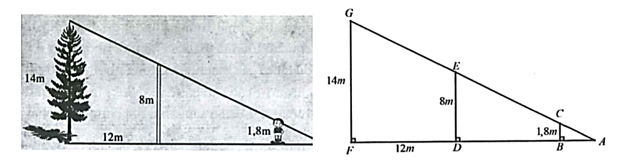
Vì \(CB \bot AF,\,\,ED \bot AF,\,\,GF \bot \,AF\) nên \(CB\parallel ED\parallel GF\).
b) Đúng.
Xét \(\Delta AFG\) có \(ED\parallel GF\) nên \(\frac{{AD}}{{AF}} = \frac{{ED}}{{GF}}\) (hệ quả của định lí Thales)
Suy ra \(\frac{{AD}}{{12}} = \frac{8}{6}\) suy ra \(AD = \frac{{12 \cdot 8}}{6} = 16\,\,\left( {\rm{m}} \right)\,\).
c) Sai.
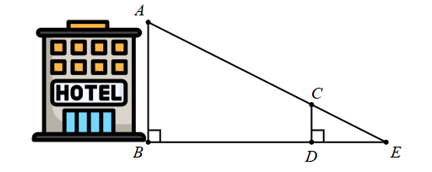
Xét \(\Delta ADE\) có \(CB\parallel ED\) nên: \(\frac{{AB}}{{AD}} = \frac{{CB}}{{ED}}\) (hệ quả của định lí Thalès)
d) Đúng.
Vì \(\frac{{AB}}{{AD}} = \frac{{CB}}{{ED}}\) nên \(\frac{{AB}}{{16}} = \frac{{1,8}}{8}\) suy ra \(AB = 3,6\,\,\left( {\rm{m}} \right)\).
Do đó, \(BD = AD - AB = 16 - 3,6 = 12,4\,\,\left( {\rm{m}} \right)\).
Vậy người quan sát có chiều cao \(1,8\,\,{\rm{m}}\) phải đứng cách bức tường \(12,4\,\,{\rm{m}}\) để có thể nhìn thấy ngọn.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập