Cho \(\alpha - \beta = \frac{\pi }{3}\). Tính giá trị của biểu thức \(A = {\left( {\cos \alpha + \cos \beta } \right)^2} + {\left( {\sin \alpha + \sin \beta } \right)^2}\).
Câu hỏi trong đề: Bài tập ôn tập Toán 11 Kết nối tri thức Chương 1 có đáp án !!
Quảng cáo
Trả lời:
\(A = {\left( {\cos \alpha + \cos \beta } \right)^2} + {\left( {\sin \alpha + \sin \beta } \right)^2}\)\( = {\cos ^2}\alpha + 2\cos \alpha \cos \beta + {\cos ^2}\beta + {\sin ^2}\alpha + 2\sin \alpha \sin \beta + {\sin ^2}\beta \)
\( = 2 + 2\left( {\cos \alpha \cos \beta + \sin \alpha \sin \beta } \right)\)\( = 2 + 2\cos \left( {\alpha - \beta } \right)\)\( = 2 + 2\cos \frac{\pi }{3} = 3\).
Trả lời: 3.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\sin \left( {x + \frac{\pi }{4}} \right) = 0\)\( \Leftrightarrow x + \frac{\pi }{4} = k\pi \)\( \Leftrightarrow x = - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
Vì \(x \in \left[ {0;2025\pi } \right]\) nên \(0 \le - \frac{\pi }{4} + k\pi \le 2025\pi \)\( \Leftrightarrow \frac{1}{4} \le k \le \frac{{8101}}{4}\) mà \(k \in \mathbb{Z}\) nên \(k \in \left\{ {1;2;..;2025} \right\}\).
Khi đó \(S = \frac{{3\pi }}{4} + \frac{{7\pi }}{4} + \frac{{11\pi }}{4} + ... + \frac{{8099\pi }}{4}\)\( = \frac{\pi }{4}\left( {3 + 7 + 11 + ... + 8099} \right)\)\( = \frac{\pi }{4}.\frac{{\left( {3 + 8099} \right).2025}}{2} = \frac{{4051.2025\pi }}{4}\).
Khi đó \(\frac{{4S}}{{2025\pi }} = \frac{4}{{2025\pi }}.\frac{{4051.2025\pi }}{4} = 4051\).
Trả lời: 4051.
Lời giải
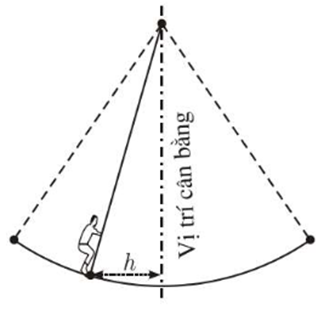
Ta có \(0 \le \left| {3\cos \frac{{\left( {2t - 1} \right)\pi }}{3}} \right| \le 3\) hay \(0 \le h \le 3\).
Đẳng thức \(h = 3\) xảy ra khi và chỉ khi \(\left| {\cos \frac{{\left( {2t - 1} \right)\pi }}{3}} \right| = 1\) \( \Leftrightarrow \sin \frac{{\left( {2t - 1} \right)\pi }}{3} = 0\)\( \Leftrightarrow \frac{{\left( {2t - 1} \right)\pi }}{3} = k\pi \)\( \Leftrightarrow 2t - 1 = 3k\)\( \Leftrightarrow t = \frac{{3k + 1}}{2}\left( {k \in \mathbb{Z},3k + 1 \ge 0} \right)\).
Ta thấy \(0 \le \frac{{3k + 1}}{2} \le 10\)\( \Leftrightarrow 0 \le 3k + 1 \le 20\)\( \Leftrightarrow - 1 \le 3k \le 19\)\( \Leftrightarrow - \frac{1}{3} \le k \le \frac{{19}}{3}\).
Mà k Î ℤ nên \(k \in \left\{ {0;1;2;3;4;5;6} \right\}\).
Các giá trị tương ứng của t là \(t \in \left\{ {\frac{1}{2};2;\frac{7}{2};5;\frac{{13}}{2};8;\frac{{19}}{2}} \right\}\).
Vậy trong khoảng thời gian 10 giây đầu tiên, có 7 lần người chơi đu ở xa vị trí cân bằng nhất.
Trả lời: 7.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) \(\sin x = - \frac{{\sqrt {10} }}{{10}}\).
b) \(\cos x = \frac{{\sqrt 3 }}{{10}}\).
c) \(\sin \left( {\frac{{4\pi }}{3} - x} \right) = - \frac{{\sqrt {10} }}{5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(x = \frac{\pi }{2} + k\pi \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(P = 2\sqrt 2 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
a) Số lượng bướm ban đầu là 5 nghìn con.
b) Số lượng bướm nhỏ nhất là 3 nghìn con.
c) Số lượng bướm luôn dao động từ 1 nghìn con đến 5 nghìn con.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.