Trong hình dưới đây, điểm nào biểu diễn số hữu tỉ \(\frac{3}{2}\) trên trục số?
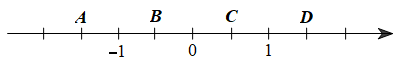
Trong hình dưới đây, điểm nào biểu diễn số hữu tỉ \(\frac{3}{2}\) trên trục số?
A. Điểm \(A\);
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Trên trục số ta thấy, đoạn thẳng đơn vị từ \( - 1\) đến 0 được chia làm 2 đoạn thẳng nhỏ bằng nhau, lấy đoạn thẳng nhỏ đó làm đoạn thẳng đơn vị mới, mỗi đoạn thẳng đơn vị mới bằng \(\frac{1}{2}\) đoạn thẳng đơn vị cũ.
Khi đó số hữu tỉ \( - \frac{3}{2}\) sẽ được biểu diễn bởi điểm nằm bên trái số 0 một đoạn bằng 3 đoạn đơn vị mới.
Vậy điểm A biểu diễn số hữu tỉ \( - \frac{3}{2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![Cho tam giác \[ABC,\]lấy \[M\] là trung điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/11-1763819910.png)
a) Xét \(\Delta AMB\) và \(\Delta DMC\) có:
\[MA = MD\] (giả thiết);
\(\widehat {AMB} = \widehat {DMC}\) (hai góc đối đỉnh);
\[MB = MC\] (do \[M\] là trung điểm của \[BC\]).
Vậy \(\Delta AMB = \Delta DMC\) (c.g.c).
b) Vì \(\Delta AMB = \Delta DMC\) (chứng minh câu a)
Nên \[AB = CD\] (hai cạnh tương ứng) và \(\widehat {ABM} = \widehat {DCM}\) (hai góc tương ứng)
Xét \(\Delta AHB\) và \(\Delta DKC\) có:
\(\widehat {AHB} = \widehat {DKC} = 90^\circ ;\)
\[AB = CD\] (chứng minh trên);
\(\widehat {ABH} = \widehat {DCK}\) (do \(\widehat {ABM} = \widehat {DCM}\)).
Do đó \[\Delta AHB = \Delta DKC\](cạnh huyền – góc nhọn).
Suy ra \[BH = CK\] (hai cạnh tương ứng).
Khi đó \[BH + HK = CK + HK\] hay \[BK = CH\].
c) Xét \[\Delta AIB\] và \[\Delta CIE\]có:
\[IA = IC\] (do \[I\] là trung điểm của \[AC\]);
\(\widehat {AIB} = \widehat {CIE}\) (hai góc đối đỉnh);
\[IB = IE\] (do \[I\] là trung điểm của \[BE\]).
Do đó \[\Delta AIB = \Delta CIE\] (c.g.c)
Suy ra \(\widehat {ABI} = \widehat {CEI}\) (hai góc tương ứng) và \[AB = CE\] (hai cạnh tương ứng).
Mà hai góc \(\widehat {ABI},\,\,\widehat {CEI}\) ở vị trí so le trong nên \[AB\,{\rm{//}}\,CE\].
Mặt khác \(\widehat {ABM} = \widehat {DCM}\) (chứng minh câu b) và hai góc này ở vị trí so le trong nên \[AB\,{\rm{//}}\,CD\].
Qua điểm \[C,\] có \[CE\,{\rm{//}}\,AB\] và \[CD\,{\rm{//}}\,AB\] nên theo tiên đề Euclid ta có \[CE\] trùng \[CD\].
Hay ba điểm \[E,{\rm{ }}C,{\rm{ }}D\] thẳng hàng.
Lại có \[CE = CD\] (cùng bằng \[AB\])
Từ đó suy ra \[C\] là trung điểm của \[DE\].
Lời giải
Cân nặng theo pound của một người nặng 45 kg là:
\(45\,\,:\,\,0,45359237\, = 99,20801798\) (pound)
Với độ chính xác \[d = 0,05\], ta làm tròn kết quả đến hàng phần mười được \(99,2\) pound.
Khi đó một người nặng 45 kg thì nặng \(99,2\) pound.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
| Loại chè | Chè thảo dược | Chè xanh | Chè đen |
| Tỉ số phần trăm (%) | 10 | 12 | 78 |
B.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Tỉ số phần trăm (%) |
12 |
10 |
78 |
C.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Tỉ số phần trăm (%) |
12 |
78 |
10 |
D.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Tỉ số phần trăm (%) |
10 |
78 |
12 |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

