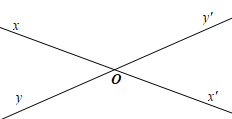
Hai đường thẳng phân biệt cắt nhau tại \(O\) nhưng không vuông góc với nhau, tạo thành bao nhiêu cặp góc đối đỉnh có số đo nhỏ hơn góc vuông?        

a) Xét \(\Delta AMB\) và \(\Delta DMC\) có:

\[MA = MD\] (giả thiết);

\(\widehat {AMB} = \widehat {DMC}\) (hai góc đối đỉnh);

\[MB = MC\] (do \[M\] là trung điểm của \[BC\]).

Vậy \(\Delta AMB = \Delta DMC\) (c.g.c).

b) Vì \(\Delta AMB = \Delta DMC\) (chứng minh câu a)

Nên \[AB = CD\] (hai cạnh tương ứng) và \(\widehat {ABM} = \widehat {DCM}\) (hai góc tương ứng)

Xét \(\Delta AHB\) và \(\Delta DKC\) có:

\(\widehat {AHB} = \widehat {DKC} = 90^\circ ;\)

\[AB = CD\] (chứng minh trên);

\(\widehat {ABH} = \widehat {DCK}\) (do \(\widehat {ABM} = \widehat {DCM}\)).

Do đó \[\Delta AHB = \Delta DKC\](cạnh huyền – góc nhọn).

Suy ra \[BH = CK\] (hai cạnh tương ứng).

Khi đó \[BH + HK = CK + HK\] hay \[BK = CH\].

c) Xét \[\Delta AIB\] và \[\Delta CIE\]có:

\[IA = IC\] (do \[I\] là trung điểm của \[AC\]);

\(\widehat {AIB} = \widehat {CIE}\) (hai góc đối đỉnh);

\[IB = IE\] (do \[I\] là trung điểm của \[BE\]).

Do đó \[\Delta AIB = \Delta CIE\] (c.g.c)

Suy ra \(\widehat {ABI} = \widehat {CEI}\) (hai góc tương ứng) và \[AB = CE\] (hai cạnh tương ứng).

Mà hai góc \(\widehat {ABI},\,\,\widehat {CEI}\) ở vị trí so le trong nên \[AB\,{\rm{//}}\,CE\].

Mặt khác \(\widehat {ABM} = \widehat {DCM}\) (chứng minh câu b) và hai góc này ở vị trí so le trong nên \[AB\,{\rm{//}}\,CD\].

Qua điểm \[C,\] có \[CE\,{\rm{//}}\,AB\] và \[CD\,{\rm{//}}\,AB\] nên theo tiên đề Euclid ta có \[CE\] trùng \[CD\].

Hay ba điểm \[E,{\rm{ }}C,{\rm{ }}D\] thẳng hàng.

Lại có \[CE = CD\] (cùng bằng \[AB\])

Từ đó suy ra \[C\] là trung điểm của \[DE\].

a) \(12:\frac{{ - 6}}{5} + \frac{1}{5} = 12.\frac{5}{{ - 6}} + \frac{1}{5} = - 10 + \frac{1}{5} = \frac{{ - 50}}{5} + \frac{1}{5} = \frac{{ - 49}}{5}\).

b) \(25.\left( { - \frac{4}{5}} \right) - 35.\left( { - \frac{4}{5}} \right)\)\[ = \frac{{ - 4}}{5}.\left( {25 - 35} \right)\]\[ = \frac{{ - 4}}{5}.\left( { - 10} \right) = 8\].

c) \(5:{\left( { - \frac{5}{2}} \right)^2} + \frac{2}{{15}}.\sqrt {\frac{9}{4}} \)\( = 5:\frac{{25}}{4} + \frac{2}{{15}}.\sqrt {{{\left( {\frac{3}{2}} \right)}^2}} \)

\( = 5.\frac{4}{{25}} + \frac{2}{{15}}.\frac{3}{2}\)\( = \frac{4}{5} + \frac{1}{5}\)\( = 1\).