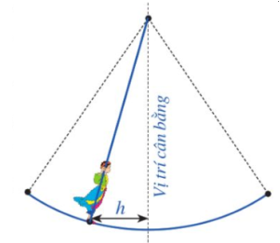
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi nhún đều, cây đu sẽ đưa người chơi dao động quanh vị trí cân bằng (hình vẽ). Nghiên cứu trò chơi này, người ta thấy khoảng cách \[h\left( m \right)\] từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian \[t\left( s \right)\] với \[t \ge 0\] bởi hệ thức \[h = \left| d \right|\] với \[d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right],\]trong đó ta quy ước \[d > 0\]khi vị trí cân bằng ở phía sau lưng người chơi đu và \[d < 0\] trong trường hợp ngược lại. Cần mất bao nhiêu thời gian tính từ lúc bắt đầu chơi đánh đu thì người chơi ở vị trí cân bằng lần thứ hai.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khi người chơi ở vị trí cân bằng thì
\[\begin{array}{l}S = 0 \Leftrightarrow 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0 \Leftrightarrow t = \frac{5}{4} + \frac{3}{2}k,k \in \mathbb{Z}\\t \ge 0 \Leftrightarrow \frac{5}{4} + \frac{3}{2}k \ge 0,k \in \mathbb{Z} \Leftrightarrow k \ge - \frac{5}{6},k \in \mathbb{Z}\end{array}\]
\[ \Rightarrow k \in \left\{ {0,1,2,3,...} \right\}\]
Khi người chơi ở vị trí cân bằng lần thứ 2 thì \[k = 1 \Rightarrow t = \frac{{11}}{4}\left( s \right)\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
D. Các cạnh bên của hình lăng trụ không bằng nhau.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập