Một rạp chiếu phim có tất cả 21 dãy ghế hàng ngang. Biết rằng dãy ghế sau cùng có 30 ghế ngồi, dãy ghế liền trước có 28 ghế ngồi,....cứ như thế dãy ghế liền trước ít hơn dãy ghế liền sau đúng 2 ghế ngồi. Suất chiếu phim vào lúc 19h00 tối 20 tháng 10 vừa qua trong rạp chỉ còn trống 10 ghế. Hỏi suất chiếu phim lúc 19h00 tối hôm đó ban tổ chức đã bán được tất cả bao nhiêu vé? Biết rằng mỗi ghế chỉ ngồi được một người và mỗi người phải mua một vé.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn D
Ta có số dãy ghế của rạp phim là cấp số cộng có 21 số hạng : \({u_1} = 30\) và \(d = - 2\).
Ta có \({S_{21}} = n{u_1} + \frac{{n\left( {n - 1} \right)d}}{2} = 21.30 + \frac{{21.20.\left( { - 2} \right)}}{2} = 210\)(ghế).
Do rạp trống 10 ghế nên rạp bán được \(200\) vé.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
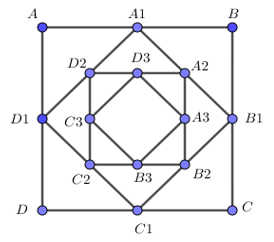
Ta có \({S_1} = {S_{ABC{\rm{D}}}} = {3^2}\);
\[{S_2} = {S_{{A_1}{B_1}{C_1}{D_1}}} = {\left( {\frac{{3\sqrt 2 }}{2}} \right)^2} = \frac{{{3^2}}}{2}\];
\({S_3} = {S_{{A_2}{B_2}{C_2}{D_2}}} = {\left( {\frac{{3\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2}} \right)^2} = \frac{{{3^2}}}{{{2^2}}}\)
………………………
\({S_n} = {3^2}\frac{1}{{{2^{n - 1}}}}\),..
Như vậy các số \({S_1},{S_2},...,{S_n},..\)lập thành một cấp số nhân lùi vô hạn có:\({S_1} = {3^2},q = \frac{1}{2}\)
Vậy \(S = {S_{ABC{\rm{D}}}} + {S_{{A_1}{B_1}{C_1}{D_1}}} + {S_{{A_2}{B_2}{C_2}{D_2}}} + ... = {S_1} + {S_2} + ... + {S_n} + ... = \frac{{{S_1}}}{{1 - q}}\)\( = \frac{{{3^2}}}{{1 - \frac{1}{2}}} = {2.3^2} = 18\).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn A
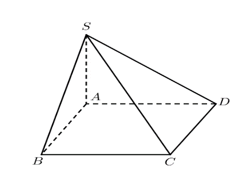
Luôn tồn tại bốn điểm không đồng phẳng là mệnh đề đúng
Có duy nhất một mặt phẳng đi qua 3 điểm không thẳng hàng nên ĐA B sai
Qua 2 điểm phân biệt có duy nhất đường thẳng đi qua nên C sai
Qua 3 điểm phân biệt không thẳng hàng có duy nhất một mặt phẳng đi qua nên D sai
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Trong không gian, cho hai đường thẳng cắt nhau a và b. Có tất cả bao nhiêu mặt phẳng chứa cả a và b?
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập