Giải các phương trình lượng giác sau

              a) \(\cos 2x = \cos \frac{\pi }{3}\).                                       b) \(\sin (x + \frac{\pi }{3}) = \frac{{\sqrt 3 }}{2}\).

a) \[\lim \frac{{8n + 5}}{{2n - 1}}\]\[ = \lim \frac{{8 + \frac{5}{n}}}{{2 - \frac{1}{n}}} = \frac{{8 + 0}}{{2 - 0}} = 4\]

              b) \[\mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^2} + 1}}{{1 - {x^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}(2 + \frac{1}{{{x^2}}})}}{{{x^2}(\frac{1}{{{x^2}}} - 1)}}\]\[ = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 + \frac{1}{{{x^2}}}}}{{\frac{1}{{{x^2}}} - 1}} = \frac{{2 + 0}}{{0 - 1}} = - 2\]

              c) \[\mathop {\lim }\limits_{x \to \sqrt 2 } \frac{{3{x^2} - 6}}{{x - \sqrt 2 }} = \mathop {\lim }\limits_{x \to \sqrt 2 } \frac{{3(x - \sqrt 2 )(x + \sqrt 2 )}}{{x - \sqrt 2 }}\]=\[\mathop {\lim }\limits_{x \to \sqrt 2 } 3(x + \sqrt 2 ) = 6\sqrt 2 \].  

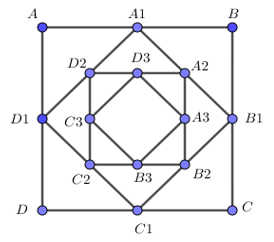
Ta có \({S_1} = {S_{ABC{\rm{D}}}} = {3^2}\);

                        \[{S_2} = {S_{{A_1}{B_1}{C_1}{D_1}}} = {\left( {\frac{{3\sqrt 2 }}{2}} \right)^2} = \frac{{{3^2}}}{2}\];

                       \({S_3} = {S_{{A_2}{B_2}{C_2}{D_2}}} = {\left( {\frac{{3\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2}} \right)^2} = \frac{{{3^2}}}{{{2^2}}}\)

                       ………………………

                       \({S_n} = {3^2}\frac{1}{{{2^{n - 1}}}}\),..

              Như vậy các số \({S_1},{S_2},...,{S_n},..\)lập thành một cấp số nhân lùi vô hạn có:\({S_1} = {3^2},q = \frac{1}{2}\)

Vậy \(S = {S_{ABC{\rm{D}}}} + {S_{{A_1}{B_1}{C_1}{D_1}}} + {S_{{A_2}{B_2}{C_2}{D_2}}} + ... = {S_1} + {S_2} + ... + {S_n} + ... = \frac{{{S_1}}}{{1 - q}}\)\( = \frac{{{3^2}}}{{1 - \frac{1}{2}}} = {2.3^2} = 18\).