Người ta giăng lưới để nuôi một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí \[A\].
![Người ta giăng lưới để nuôi một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí \[A\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/50-1764858038.png)
Hỏi diện tích nhỏ nhất có thể giăng khu nuôi cá riêng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là \[5\,\,{\rm{m}}\] và khoảng cách từ cọc đến bờ dọc là \[12\,\,{\rm{m?}}\]
Người ta giăng lưới để nuôi một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí \[A\].
Hỏi diện tích nhỏ nhất có thể giăng khu nuôi cá riêng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là \[5\,\,{\rm{m}}\] và khoảng cách từ cọc đến bờ dọc là \[12\,\,{\rm{m?}}\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đặt tên các đỉnh như hình vẽ. Đặt \[CJ = x\,\,\left( {{\rm{m}},\,x > 0} \right)\].
![Người ta giăng lưới để nuôi một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí \[A\]. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/51-1764858058.png)
Chứng minh được tam giác \[AJC\] và \[BKA\] là hai tam giác đồng dạng nên
\[\frac{{CJ}}{{AK}} = \frac{{JA}}{{KB}}\] hay \[\frac{x}{5} = \frac{{12}}{{KB}}\] do đó \[KB = \frac{{60}}{x}\].
Diện tích của khu nuôi cá là \[S\left( x \right) = \frac{1}{2}\left( {x + 5} \right)\left( {\frac{{60}}{x} + 12} \right)\]
\[S\left( x \right) = \frac{1}{2}\left( {60 + 12x + \frac{{300}}{x} + 60} \right)\]
\[S\left( x \right) = 6x + \frac{{150}}{x} + 60 = 6\left( {x + \frac{{25}}{x} + 10} \right) = 6\left( {\frac{{{x^2} - 10x + 25}}{x} + 20} \right) = 6\left[ {\frac{{{{\left( {x - 5} \right)}^2}}}{x} + 20} \right] \ge 120\].
Dấu “=” xảy ra khi \[x - 5 = 0\] nên \[x = 5.\]
Vậy diện tích nhỏ nhất có thể giăng là \[120\,\,{{\rm{m}}^2},\] đạt được khi \[x = 5\;\left( {\rm{m}} \right)\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
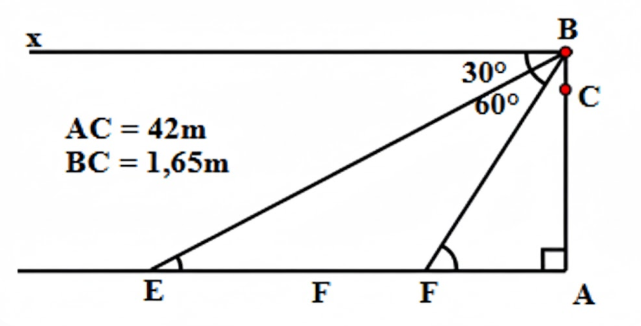
Ta có \[\widehat {BEF} = \widehat {xBE} = 30^\circ \] (Vì \[Bx\parallel AF\] và hai góc ở vị trí so le trong).
\[\widehat {BFA} = \widehat {xBF} = 60^\circ \].
Xét tam giác vuông \[ABF\] có \[\widehat {FBA} = 30^\circ \] suy ra \[AF = \frac{1}{2}BF.\]
Áp dụng định lí Pythagore vào tam giác vuông \[ABF\] có:
\[A{B^2} + A{F^2} = B{F^2}\]
\[A{B^2} + A{F^2} = {\left( {2AF} \right)^2}\]
\[A{B^2} = 3A{F^2}\]
\[{\left( {AC + BC} \right)^2} = 3A{F^2}\]
\[{\left( {42 + 1,65} \right)^2} = 3A{F^2}\]
\[43,{65^2} = 3A{F^2}\]
\[AF = \sqrt {\frac{{43,{{65}^2}}}{3}} \]
\[AF \approx 25,2\,\,{\rm{m}}{\rm{.}}\]
Xét \[\Delta ABF\] và \[\Delta AEB\] có:
\[\widehat {ABF} = \widehat {AEB} = 30^\circ \]
\[\widehat A\] chung
Do đó, (g.g).
Suy ra \[\frac{{AF}}{{AB}} = \frac{{AB}}{{AE}}\], do đó \[AE = \frac{{A{B^2}}}{{AF}} = \frac{{43,{{65}^2}}}{{25,2}} = 75,6{\rm{ }}\left( {{\rm{cm}}} \right)\].
Sau hai lần quan sát, tàu đã chạy được: \[75,6 - 25,5 = 50,4\,\,\left( {\rm{m}} \right)\].
Lời giải
Hướng dẫn giải
a) Ta có: \(A = \frac{{{x^3} + {y^3} + {z^3} - 3xyz}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}}\)
\( = \frac{{{{\left( {x + y} \right)}^3} - 3xy\left( {x + y} \right) + {z^3} - 3xyz}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}}\)
\( = \frac{{{{\left( {x + y} \right)}^3} + {z^3} - 3xy\left( {x + y + z} \right)}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}}\)
\( = \frac{{{{\left( {x + y + z} \right)}^3} - 3\left( {x + y} \right)z\left( {x + y + z} \right) - 3xy\left( {x + y + z} \right)}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}}\)
\[ = \frac{{\left( {x + y + z} \right)\left[ {{{\left( {x + y + z} \right)}^2} - 3\left( {x + y} \right)z - 3xy} \right]}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}}\]
\[ = \frac{{\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} + 2xy + 2yz + 2zx - 3xz - 3yz - 3xy} \right)}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}}\]
\[ = \frac{{\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - yz - zx} \right)}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}} = x + y + z.\]
b) Ta có: \(B = \frac{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}{{{x^{26}} + {x^{24}} + {x^{22}} + ... + {x^2} + 1}},\) xét phân thức nghịch đảo của phân thức \(B\) là:
\(\frac{1}{B} = \frac{{{x^{26}} + {x^{24}} + {x^{22}} + ... + {x^2} + 1}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{\left( {{x^{26}} + {x^{22}} + {x^{18}} + ... + {x^6} + {x^2}} \right) + \left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{{x^2}\left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right) + \left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{\left( {{x^{24}} + {x^{20}} + ... + 1} \right)\left( {{x^2} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}} = {x^2} + 1.\)
Vậy \(B = \frac{1}{{{x^2} + 1}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập