Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận \(y\) (đồng) theo công thức sau: \(y = - 86{x^2} + 86000x - 18146000\), trong đó \(x\) là số sản phẩm được bán ra.
a) Doanh nghiệp bị lỗ khi bán từ 303 đến 698 sản phẩm.
b) Doanh nghiệp có lãi khi bán tối đa 302 sản phẩm hoặc bán tối thiểu 697 sản phẩm
c) Doanh nghiệp có lãi khi bán từ 303 đến 697 sản phẩm.
d) Doanh nghiệp bị lỗ khi bán tối đa 302 sản phẩm hoặc bán tối thiểu 698 sản phẩm
Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận \(y\) (đồng) theo công thức sau: \(y = - 86{x^2} + 86000x - 18146000\), trong đó \(x\) là số sản phẩm được bán ra.
a) Doanh nghiệp bị lỗ khi bán từ 303 đến 698 sản phẩm.
b) Doanh nghiệp có lãi khi bán tối đa 302 sản phẩm hoặc bán tối thiểu 697 sản phẩm
c) Doanh nghiệp có lãi khi bán từ 303 đến 697 sản phẩm.
d) Doanh nghiệp bị lỗ khi bán tối đa 302 sản phẩm hoặc bán tối thiểu 698 sản phẩm
Quảng cáo
Trả lời:
Xét tam thức bậc hai \(f(x) = - 86{x^2} + 86000x - 18146000\).
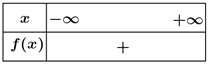
Nhận thấy \(f(x) = 0\) có hai nghiệm là \({x_1} \approx 302,5;\,\,\,\,\,\,\,{x_2} \approx 697,5\) và hệ số \(a = - 86 < 0\). Ta có bảng xét dấu sau:

Vì \(x\) là số nguyên dương nên:
Doanh nghiệp có lãi khi và chỉ khi \(f(x) > 0\), tức là \(303 \le x \le 697\).
Doanh nghiệp bị lỗ khi và chỉ khi \(f(x) < 0\), tức là \(x \le 302\) hoặc \(x \ge 698\).
Vậy doanh nghiệp có lãi khi bán từ 303 đến 697 sản phẩm, doanh nghiệp bị lỗ khi bán tối đa 302 sản phẩm hoặc bán tối thiểu 698 sản phẩm.
a) Sai: Doanh nghiệp bị lỗ khi bán từ 303 đến 698 sản phẩm.
b) Sai: Doanh nghiệp có lãi khi bán tối đa 302 sản phẩm hoặc bán tối thiểu 697 sản phẩm
c) Đúng: Doanh nghiệp có lãi khi bán từ 303 đến 697 sản phẩm.
d) Đúng: Doanh nghiệp bị lỗ khi bán tối đa 302 sản phẩm hoặc bán tối thiểu 698 sản phẩm
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng: Số cách gieo lần một là 6 cách, số cách gieo lần hai là 1 cách. Suy ra số cách để sau hai lần gieo đều ra số chấm giống nhau là \(6.1 = 6\) cách.
b) Đúng: Số cách gieo lần một xuất hiện mặt 6 chấm là 1 cách, lần gieo thứ hai có 6 cách. Suy ra số cách gieo để gieo được lần đầu ra mặt 6 chấm là \(6.1 = 6\) cách.
c) Sai: Số cách gieo lần một được mặt 1 chấm là 1 cách, lần hai được mặt có số chấm khác 1 là 5 cách.
Số cách gieo lần một được mặt có số chấm khác 1 là 5 cách, lần hai được mặt 1 chấm là 1 cách.
Vậy số cách để hai lần gieo xuất hiện đúng một lần mặt 1 chấm là \(1.5 + 5.1 = 10\) cách.
d) Đúng: Số cách gieo hai lần là \(6.6 = 36\) cách.
Trường hợp 1: Số cách gieo hai lần đều được mặt 1 chấm là 1 cách.
Trường hợp 2: Số cách gieo hai lần được tổng số chấm bằng 3 là: 2 cách, gồm \(\left( {1;2} \right),\left( {2;1} \right)\).
Vậy số cách để sau hai lần gieo được tổng số chấm nhỏ hơn 4 là \(2 + 1 = 3\) cách.
Số cách gieo để sau hai lần gieo được tổng số chấm không bé hơn 4 là \(36 - 3 = 33\) cách.
Câu 2
Lời giải
Đáp án đúng là C
Không gian mẫu có \(A_{35}^3\) phần tử.
Có \(15\) cách chọn 1 học sinh nam và \(C_{20}^2\) cách chọn 2 học sinh nữ vào ban cán sự.
Sau khi chọn được 3 người, có \(3!\) cách phân chức vụ.
Suy ra có \(3!.15.C_{20}^2\) cách chọn ban cán sự lớp theo yêu cầu.
Vậy xác suất cần tính là \(\frac{{3!.15.C_{20}^2}}{{A_{35}^3}} = \frac{{570}}{{1309}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.