PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho phương trình \[{9^{x + 1}} - {13.6^x} + {4^{x + 1}} = 0\]. Xét tính đúng sai của các mệnh đề sau

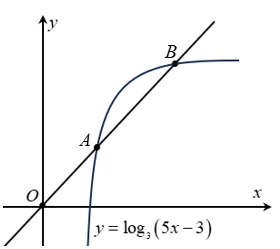
Gọi \[A\left( {{x_1},{{\log }_3}\left( {5{x_1} - 3} \right)} \right)\]. Vì \[A\] là trung điểm \[OB\] nên \[B\left( {2{x_1};2{{\log }_3}\left( {5{x_1} - 3} \right)} \right)\].

Vì \[B\] thuộc đồ thị của hàm số \[y = {\log _3}\left( {5x - 3} \right)\] nên \[2{\log _3}\left( {5{x_1} - 3} \right) = {\log _3}\left( {10{x_1} - 3} \right) \Leftrightarrow \left\{ \begin{array}{l}5{x_1} - 3 > 0\\10{x_1} - 3 > 0\\{\left( {5{x_1} - 3} \right)^2} = 10{x_1} - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5{x_1} - 3 > 0\\\left[ \begin{array}{l}x = \frac{6}{5}\\x = \frac{2}{5}\end{array} \right.\end{array} \right. \Leftrightarrow {x_1} = \frac{6}{5}\].

Vì thế \[A\left( {\frac{6}{5};1} \right),\,B\left( {\frac{{12}}{5};2} \right) \Rightarrow AB = \frac{{\sqrt {61} }}{5}\].

Hình chiếu điểm \(B\) xuống trục hoành là \(H\left( {\frac{{12}}{5};\,0} \right) \Rightarrow BH = 2\) và \(OH = \frac{{12}}{5} \Rightarrow {S_{\Delta OBH}} = \frac{{12}}{5}\)

a) Đúng: Hoành độ của điểm \(B\) là một số nguyên.

b) Sai: Trung điểm của đoạn thẳng \(OB\) là điểm \(A\) có tọa độ \(\left( {\frac{6}{5};\,1} \right)\).

c) Sai: Gọi \(H\) là hình chiếu của điểm \(B\) xuống trục hoành. Khi đó \({S_{\Delta OBH}} = \frac{{12}}{5}\)

d) Đúng: Đoạn thẳng \(AB\) có độ dài bằng \[\frac{{\sqrt {61} }}{5}\].

Theo hình thức lãi kép, tổng số tiền cả gốc lẫn lãi trong tài khoản của người đó sau \[n\] tháng là:

\[A = 200{\left( {1 + 0,58\% } \right)^n} = 200.1,{0058^n}\] (triệu đồng).

Theo đề bài \[A \ge 225 \Rightarrow 200.1,{0058^n} \ge 225 \Leftrightarrow 1,{0058^n} \ge \frac{9}{8}\]\[ \Leftrightarrow n \ge {\log _{1,0058}}\frac{9}{8} \approx 20,37\].

Vì ngân hàng chỉ tính lãi khi đến kì hạn nên phải sau ít nhất 21 tháng người đó mới có tối thiểu 225 triệu đồng trong tài khoản.