Một cái hộp hình lập phương, bên trong nó đựng một mô hình đồ chơi có dạng hình chóp tứ giác đều mà đỉnh của hình chóp đó trùng với tâm của một mặt chiếc hộp, giả sử hình vuông đáy của hình chóp trùng với một mặt của chiếc hộp (mặt này cùng với mặt chứa đỉnh hình chóp là hai mặt đối nhau). Biết cạnh của chiếc hộp bằng \(30\;cm\), hãy tính thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp (mô hình đồ chơi được làm bởi chất liệu nhựa đặc bên trong).
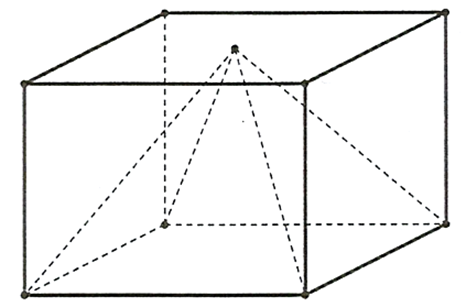
Một cái hộp hình lập phương, bên trong nó đựng một mô hình đồ chơi có dạng hình chóp tứ giác đều mà đỉnh của hình chóp đó trùng với tâm của một mặt chiếc hộp, giả sử hình vuông đáy của hình chóp trùng với một mặt của chiếc hộp (mặt này cùng với mặt chứa đỉnh hình chóp là hai mặt đối nhau). Biết cạnh của chiếc hộp bằng \(30\;cm\), hãy tính thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp (mô hình đồ chơi được làm bởi chất liệu nhựa đặc bên trong).

Quảng cáo
Trả lời:
Trả lời: \(18000\left( {\;c{m^3}} \right)\)
Lời giải
Thể tích cái hộp (khối lập phương) là: \({V_1} = {30^3} = 27000\left( {\;c{m^3}} \right)\).
Xét đồ chơi có dạng hình chóp tứ giác đều, chiều cao của hình chóp bằng với một cạnh của hình lập phương, hay \(h = 30\;cm\), đáy của hình chóp có diện tích \(S = {30^2} = 900\;c{m^2}\).
Thể tích khối đồ chơi (khối chóp tứ giác đều) là:
\({V_2} = \frac{1}{3}Sh = \frac{1}{3} \cdot 900 \cdot 30 = 9000\left( {\;c{m^3}} \right){\rm{. }}\)
Thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp: \(V = {V_1} - {V_2} = 27000 - 9000 = 18000\left( {\;c{m^3}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) \(x = \frac{{3a}}{4}\).
b)\(y = 2x\).
c) \(y = z + x\).
Lời giải
|
a) Sai |
b) Đúng |
c) Sai |
d) Đúng |
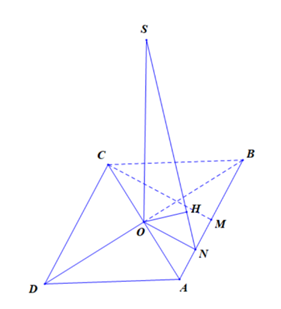
Tam giác \(ABC\) đều cạnh \(a\) nên đường cao \(CM = \frac{{a\sqrt 3 }}{2}\). Gọi \(N\) là trung điểm của \(AM\) \( \Rightarrow ON \bot AB;ON = \frac{{a\sqrt 3 }}{4}\).
Kẻ \(OH \bot SN\)\( \Rightarrow d\left( {O,\left( {SAB} \right)} \right) = OH\).
\[\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{N^2}}}\]; \[ON = \frac{1}{2}CM = \frac{{a\sqrt 3 }}{4}\]; \[SO = \frac{{3a}}{4} \Rightarrow OH = \frac{{3a}}{8}\].
\(x = d\left( {O,\left( {SAB} \right)} \right) = \frac{{3a}}{8}\), \(y = d\left( {D,\left( {SAB} \right)} \right) = 2.d\left( {O,\left( {SAB} \right)} \right) = 2x\), \(z = d\left( {CD,SA} \right)\)\( = d\left( {D,\left( {SAB} \right)} \right) = 2x\).
Vậy \(x + y + z = 5x = \frac{{15a}}{8}\).
Lời giải
Trả lời: \( \approx {51,14^^\circ }\)
Lời giải
Trong mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }{D^\prime }} \right)\), kẻ \({A^\prime }H \bot {B^\prime }{D^\prime }\) tại \(H\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{B^\prime }{D^\prime } \bot {A^\prime }H}\\{{B^\prime }{D^\prime } \bot A{A^\prime }\left( {{\rm{do }}A{A^\prime } \bot \left( {{A^\prime }{B^\prime }{C^\prime }{D^\prime }} \right)} \right)}\end{array} \Rightarrow {B^\prime }{D^\prime } \bot \left( {A{A^\prime }H} \right) \Rightarrow {B^\prime }{D^\prime } \bot AH} \right.\).
Do đó \(\widehat {AH{A^\prime }}\) là góc phẳng nhị diện \(\left[ {A,{B^\prime }{D^\prime },{A^\prime }} \right]\).
![Một hộp phấn không bụi có dạng hình hộp chữ nhật, chiều cao hộp phấn bằng 8,2cm và đáy của nó có hai kích thước là 8,5cm;10,5cm (xem hình vẽ sau). Tìm góc phẳng nhị diện [A,B'D',A'] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid6-1765851742.png)
Tam giác \({A^\prime }{B^\prime }{D^\prime }\) vuông tại \({A^\prime }\) có đường cao \({A^\prime }H\) nên
\(\frac{1}{{{A^\prime }{H^2}}} = \frac{1}{{{A^\prime }{B^{\prime 2}}}} + \frac{1}{{{A^\prime }{D^{\prime 2}}}} \Rightarrow {A^\prime }H = \frac{{{A^\prime }{B^\prime } \cdot {A^\prime }{D^\prime }}}{{\sqrt {{A^\prime }{B^{\prime 2}} + {A^\prime }{D^{\prime 2}}} }} = \frac{{357}}{{2\sqrt {730} }}{\rm{. }}\)
Tam giác \(AH{A^\prime }\) vuông tại \({A^\prime }\) có:
\(\tan \widehat {AH{A^\prime }} = \frac{{A{A^\prime }}}{{{A^\prime }H}} = \frac{{8,2}}{{\frac{{357}}{{2\sqrt {730} }}}} \Rightarrow \widehat {AH{A^\prime }} \approx {51,14^^\circ }\)
Câu 3
a) Ta có \[\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = 2\]
b) Với \(a = - 2\) thì hàm số có đạo hàm tại \[x = 1\]
c) Với \(a = 2\) thì hàm số có đạo hàm tại \[x = 1\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Đường thẳng \(y = 0\) cắt đồ thị hàm số \(\left( C \right)\) tại điểm có hoành độ là \(x = {\log _3}2\).
b) Bất phương trình \(f\left( x \right) \ge - 1\) có nghiệm duy nhất.
c) Bất phương trình \(f\left( x \right) \ge 0\) có tập nghiệm là: \(\left( { - \infty ;{{\log }_3}2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là: \(\frac{{273}}{{800}}{\rm{. }}\)
b) Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là: \(\frac{{89}}{{160}}{\rm{. }}\)
c) Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường thuận tay trái lần lượt là: \(\frac{{11}}{{160}}{\rm{ v\`a }}\frac{{27}}{{800}}{\rm{. }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một hộp phấn không bụi có dạng hình hộp chữ nhật, chiều cao hộp phấn bằng 8,2cm và đáy của nó có hai kích thước là 8,5cm;10,5cm (xem hình vẽ sau). Tìm góc phẳng nhị diện [A,B'D',A'] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid7-1765851756.png)