Theo số liệu của tổng cục thống kê, dân số Việt Nam năm 2015 là \(91,7\) triệu người. Giả sử tỉ lệ tăng dân số hàng năm của Việt Nam trong giai đoạn 2015-2040 ở mức không đổi \(1,1\% \). Hỏi đến năm bao nhiêu dân số Việt Nam đạt mức \(113\) triệu người?
Quảng cáo
Trả lời:
Trả lời: 2034
Lời giải
Giả sử sau \(n\) năm dân số Việt Nam là \({113.10^6}\) ( người).
\( \Rightarrow {113.10^6} = {91,7.10^6}.{\left( {1 + 1,1\% } \right)^n}\) \( \Leftrightarrow {\left( {1,01} \right)^n} = \frac{{1130}}{{917}} \Leftrightarrow n = {\log _{1,011}}\frac{{1130}}{{917}} = 19\)
Vậy đến năm 2034 thì dân số Việt Nam là \(113\) triệu người.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) Ta có \[\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = 2\]
b) Với \(a = - 2\) thì hàm số có đạo hàm tại \[x = 1\]
c) Với \(a = 2\) thì hàm số có đạo hàm tại \[x = 1\]
Lời giải
|
a) Đúng |
b) Sai |
c) Đúng |
d) Đúng |
Để hàm số có đạo hàm tại \[x = 1\] thì trước hết \[f(x)\] phải liên tục tại \[x = 1\]
Hay \[\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = 2 = f(1) = a\].
Khi đó, ta có:\[\mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{{{x^2} - 1}}{{x - 1}} - 2}}{{x - 1}} = 1\].
Vậy \[a = 2\] là giá trị cần tìm.
Câu 2
a) \(x = \frac{{3a}}{4}\).
b)\(y = 2x\).
c) \(y = z + x\).
Lời giải
|
a) Sai |
b) Đúng |
c) Sai |
d) Đúng |
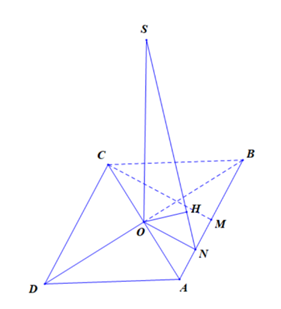
Tam giác \(ABC\) đều cạnh \(a\) nên đường cao \(CM = \frac{{a\sqrt 3 }}{2}\). Gọi \(N\) là trung điểm của \(AM\) \( \Rightarrow ON \bot AB;ON = \frac{{a\sqrt 3 }}{4}\).
Kẻ \(OH \bot SN\)\( \Rightarrow d\left( {O,\left( {SAB} \right)} \right) = OH\).
\[\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{N^2}}}\]; \[ON = \frac{1}{2}CM = \frac{{a\sqrt 3 }}{4}\]; \[SO = \frac{{3a}}{4} \Rightarrow OH = \frac{{3a}}{8}\].
\(x = d\left( {O,\left( {SAB} \right)} \right) = \frac{{3a}}{8}\), \(y = d\left( {D,\left( {SAB} \right)} \right) = 2.d\left( {O,\left( {SAB} \right)} \right) = 2x\), \(z = d\left( {CD,SA} \right)\)\( = d\left( {D,\left( {SAB} \right)} \right) = 2x\).
Vậy \(x + y + z = 5x = \frac{{15a}}{8}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
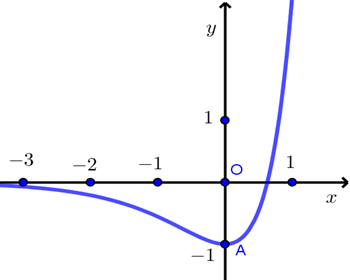
a) Đường thẳng \(y = 0\) cắt đồ thị hàm số \(\left( C \right)\) tại điểm có hoành độ là \(x = {\log _3}2\).
b) Bất phương trình \(f\left( x \right) \ge - 1\) có nghiệm duy nhất.
c) Bất phương trình \(f\left( x \right) \ge 0\) có tập nghiệm là: \(\left( { - \infty ;{{\log }_3}2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là: \(\frac{{273}}{{800}}{\rm{. }}\)
b) Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là: \(\frac{{89}}{{160}}{\rm{. }}\)
c) Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường thuận tay trái lần lượt là: \(\frac{{11}}{{160}}{\rm{ v\`a }}\frac{{27}}{{800}}{\rm{. }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một hộp phấn không bụi có dạng hình hộp chữ nhật, chiều cao hộp phấn bằng 8,2cm và đáy của nó có hai kích thước là 8,5cm;10,5cm (xem hình vẽ sau). Tìm góc phẳng nhị diện [A,B'D',A'] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid7-1765851756.png)