Cho phương trình: \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 8 = 0\). (\(m\) là tham số).
1) Tìm các giá trị của tham số \(m\) để phương trình đã cho có nghiệm bằng 2.
2) Tìm các giá trị của tham số \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện \(4{x_1} - 3{x_2} = 25\).
Cho phương trình: \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 8 = 0\). (\(m\) là tham số).
1) Tìm các giá trị của tham số \(m\) để phương trình đã cho có nghiệm bằng 2.
2) Tìm các giá trị của tham số \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện \(4{x_1} - 3{x_2} = 25\).
Quảng cáo
Trả lời:
1) Để phương trình có nghiệm bằng 2, thay \(x = 2\) vào phương trình, ta được:
\({2^2} - 2\left( {m - 2} \right) \cdot 2 + {m^2} - 8 = 0\) hay \(4 - 4m + 8 + {m^2} - 8 = 0\).
Khi đó \({m^2} - 4m + 4 = 0\) hay \({\left( {m - 2} \right)^2} = 0\) nên \(m = 2\).
Vậy \(m = 2\) thì phương trình có nghiệm \(x = 2\)
2) \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 8 = 0 & \left( 1 \right)\)
Ta có \[\Delta = 4{\left( {m - 2} \right)^2} - 4\left( {{m^2} - 8} \right) = 4{m^2} - 16m + 16 - 4{m^2} + 32 = - 32m + 48\].
Để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt thì \[\Delta > 0\] hay \[ - 32m + 48 > 0\] nên \[m < 3.\]
Khi đó \(\left( 1 \right)\) có hai nghiệm phân biệt \[{x_1},{\rm{ }}{x_2}.\]
Áp dụng hệ thức Viète, ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m - 2} \right)}\\{{x_1}{x_2} = {m^2} - 8}\end{array}} \right.\).
Để \(4{x_1} - 3{x_2} = 25\) thì \(\left\{ {\begin{array}{*{20}{l}}{4{x_1} - 3{x_2} = 25}\\{{x_1} + {x_2} = 2m - 4\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\).
Nhân hai vế của phương trình \[\left( 2 \right)\] với 4, ta được hệ: \(\left\{ {\begin{array}{*{20}{l}}{4{x_1} - 3{x_2} = 25 & & \left( 3 \right)}\\{4{x_1} + 4{x_2} = 8m - 16 & \left( 4 \right)}\end{array}} \right..\)
Trừ từng vế phương trình \(\left( 4 \right)\) cho \(\left( 3 \right)\) ta được: \(7{x_2} = 8m - 41\), tức là \({x_2} = \frac{{8m - 41}}{7}.\)
Thế \({x_2} = \frac{{8m - 41}}{7}\) vào phương trình \[\left( 2 \right)\] ta có: \({x_1} + \frac{{8m - 41}}{7} = 2m - 4\) hay \({x_1} = \frac{{6m + 13}}{7}.\)
Thay \({x_1} = \frac{{6m + 13}}{7}\,;\,\,{x_2} = \frac{{8m - 41}}{7}\) vào \({x_1}{x_2} = {m^2} - 8\) ta được
\(\frac{{6m + 13}}{7} \cdot \frac{{8m - 41}}{7} = {m^2} - 8\)
\(\frac{{\left( {6m + 13} \right)\left( {8m - 41} \right)}}{{49}} = {m^2} - 8\)
\[\left( {6m + 13} \right)\left( {8m - 41} \right) = 49\left( {{m^2} - 8} \right)\]
\(48{m^2} - 142m - 533 = 49{m^2} - 392\)
\({m^2} + 142m + 141 = 0\).
Ta thấy \(1 - 142 + 141 = 0\) nên phương trình có nghiệm \(m = - 1\) hoặc \(m = - 141\) (thỏa mãn \(m < 3).\)
Vậy \[m \in \left\{ { - 1\,;\,\, - 141} \right\}\] thì phương trình đã cho có hai nghiệm phân biệt \({x_1}\), \({x_2}\) thỏa mãn điều kiện \(4{x_1} - 3{x_2} = 25.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
1) Do \(\widehat {AMB} = \widehat {ANB} = 90^\circ \) (các góc nội tiếp chắn nửa đường tròn) nên \(\widehat {CMB} = \widehat {CND} = 90^\circ .\) Xét tứ giác \[CMDN\] có \[\widehat {CMD} + \widehat {CND} = 90^\circ + 90^\circ = 180^\circ .\] Mà hai góc này ở vị trí đối diện nên tứ giác \[CMDN\] nội tiếp được trong đường tròn. |
![Cho đường tròn tâm \(O\) đường kính \[AB\] và \(M\) là điểm chính giữa của cung (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid3-1766238737.png) |
2) Xét \(\Delta AMD\) và \(\Delta ANC\) có \(\widehat {NAC}\) chung; \(\widehat {AMD} = \widehat {ANC} = 90^\circ .\)
Do đó , suy ra \(\frac{{AM}}{{AN}} = \frac{{AD}}{{AC}}\) hay \(AM \cdot AC = AN \cdot AD\).
3) Do \[ABNM\] nội tiếp \(\left( O \right)\) nên \(\widehat {BAM} + \widehat {BNM} = 180^\circ \).
Mà \(\widehat {BNM} + \widehat {CNM} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CNM} = \widehat {BAM}\).
Mà \[\widehat {CNM} = \widehat {MCD}\] (góc nội tiếp cùng chắn cung
Suy ra \(\widehat {MCD} = \widehat {OMB}\,\,\left( { = \widehat {CNM}} \right)\) hay \(\widehat {MCD} = \widehat {OMB}.\)
4) Do \[M\] là điểm chính giữa cung \[AB\] nên \(MA = MB\).
Suy ra \(\widehat {MNA} = \widehat {MAB}\) (góc nội tiếp chắn hai cung bằng nhau).
Xét \(\Delta MAN\) và \(\Delta MAE\) có \(\widehat {AME}\) chung; \(\widehat {MNA} = \widehat {MAE}\,\,({\rm{cmt}})\).
Do đó .
Suy ra \(\widehat {MAN} = \widehat {MEA}\) (hai góc tương ứng).
Mà \[\widehat {MAN} = \widehat {MBN}\] (góc nội tiếp cùng chắn nên \(\widehat {MBN} = \widehat {MEB}\).
Do đó \(\widehat {DBN} = \widehat {NEB}\) (đpcm).
Lời giải
|
1) Vẽ đồ thị của hàm số \(y = \frac{3}{4}{x^2}\). Tập xác định \(D = \mathbb{R}\). Bảng giá trị:
Đồ thị hàm số \(y = \frac{3}{4}{x^2}\) là Parabol nhận \[Oy\] làm trục đối xứng, có đỉnh \(O\left( {0\,;\,\,0} \right)\), bề lõm hướng lên và đi qua các điểm \(\left( { - 1\,;\,\,\frac{3}{4}} \right),\,\,\left( {1\,;\,\,\frac{3}{4}} \right),\,\)\(\,\left( { - 2\,;\,\,3} \right),\,\,\left( {2\,;\,\,3} \right).\) |
Ta có đồ thị hàm số 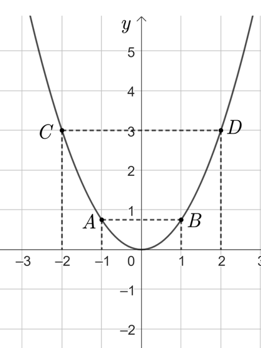
|
2) Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm của phương trình:
\(\frac{3}{4}{x^2} = x + m\) hay \(\frac{3}{4}{x^2} - x - m = 0\).
Để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt thì phương trình trên phải có hai nghiệm phân biệt
Hay \(\Delta = {( - 1)^2} - 4 \cdot \frac{3}{4}( - m) = 1 + 3m > 0\) hay \(m > \frac{{ - 1}}{3}\).
Vậy với \(m > \frac{{ - 1}}{3}\) thì \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.