Một khu vườn hình chữ nhật có chu vi \[200{\rm{ m}}.\] Do mở rộng đường giao thông nông thôn nên chiều dài khu vườn giảm \[8{\rm{ m}}.\] Tính chiều dài và chiều rộng của khu vườn ban đầu, biết diện tích đất còn lại để trồng cây là \(2\,080\;\,{{\rm{m}}^2}\).
Một khu vườn hình chữ nhật có chu vi \[200{\rm{ m}}.\] Do mở rộng đường giao thông nông thôn nên chiều dài khu vườn giảm \[8{\rm{ m}}.\] Tính chiều dài và chiều rộng của khu vườn ban đầu, biết diện tích đất còn lại để trồng cây là \(2\,080\;\,{{\rm{m}}^2}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \[x\,\,\left( {\rm{m}} \right)\] là chiều dài ban đầu của khu vườn hình chữ nhật \[\left( {0 < x < 100} \right)\].
Khi đó nửa chu vi khu vườn hình chữ nhật là: \(200:2 = 100\,\,\left( m \right).\)
Chiều rộng ban đầu của khu vườn là \(100 - x\,\,\left( {\rm{m}} \right)\).
Chiều dài khu vườn sau khi giảm \(8\,\,{\rm{m}}\) là \(x - 8\,\,\left( {\rm{m}} \right)\).
Diện tích của khu vườn sau khi giảm là: \[\left( {x - 8} \right)\left( {100 - x} \right) = 2\,\,080\]
\[ - {x^2} + 108x - 800 = 2\,\,080\]
\[{x^2} - 108x + 2\,\,880 = 0\]
\(x = 60\) hoặc \(x = 48\).
• Với \(x = 60\) hay chiều dài ban đầu của khu vườn là \(60\,\,{\rm{m}}\) thì
Chiều rộng ban đầu của khu vườn là \(100 - 60 = 40\,\,\left( {\rm{m}} \right)\) (thỏa mãn).
• Với \(x = 48\) hay chiều dài ban đầu của khu vườn là \(60\,\,{\rm{m}}\) thì
Chiều rộng ban đầu của khu vườn là \(100 - 48 = 52\,\,\left( {\rm{m}} \right)\) (loại vì chiều dài phải lớn hơn chiều rộng).
Vậy chiều dài ban đầu của khu vườn là \(60\,\,{\rm{m}}\) và chiều rộng ban đầu của khu vườn là \(40\,\,{\rm{m}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
1) Do \(\widehat {AMB} = \widehat {ANB} = 90^\circ \) (các góc nội tiếp chắn nửa đường tròn) nên \(\widehat {CMB} = \widehat {CND} = 90^\circ .\) Xét tứ giác \[CMDN\] có \[\widehat {CMD} + \widehat {CND} = 90^\circ + 90^\circ = 180^\circ .\] Mà hai góc này ở vị trí đối diện nên tứ giác \[CMDN\] nội tiếp được trong đường tròn. |
![Cho đường tròn tâm \(O\) đường kính \[AB\] và \(M\) là điểm chính giữa của cung (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid3-1766238737.png) |
2) Xét \(\Delta AMD\) và \(\Delta ANC\) có \(\widehat {NAC}\) chung; \(\widehat {AMD} = \widehat {ANC} = 90^\circ .\)
Do đó , suy ra \(\frac{{AM}}{{AN}} = \frac{{AD}}{{AC}}\) hay \(AM \cdot AC = AN \cdot AD\).
3) Do \[ABNM\] nội tiếp \(\left( O \right)\) nên \(\widehat {BAM} + \widehat {BNM} = 180^\circ \).
Mà \(\widehat {BNM} + \widehat {CNM} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CNM} = \widehat {BAM}\).
Mà \[\widehat {CNM} = \widehat {MCD}\] (góc nội tiếp cùng chắn cung
Suy ra \(\widehat {MCD} = \widehat {OMB}\,\,\left( { = \widehat {CNM}} \right)\) hay \(\widehat {MCD} = \widehat {OMB}.\)
4) Do \[M\] là điểm chính giữa cung \[AB\] nên \(MA = MB\).
Suy ra \(\widehat {MNA} = \widehat {MAB}\) (góc nội tiếp chắn hai cung bằng nhau).
Xét \(\Delta MAN\) và \(\Delta MAE\) có \(\widehat {AME}\) chung; \(\widehat {MNA} = \widehat {MAE}\,\,({\rm{cmt}})\).
Do đó .
Suy ra \(\widehat {MAN} = \widehat {MEA}\) (hai góc tương ứng).
Mà \[\widehat {MAN} = \widehat {MBN}\] (góc nội tiếp cùng chắn nên \(\widehat {MBN} = \widehat {MEB}\).
Do đó \(\widehat {DBN} = \widehat {NEB}\) (đpcm).
Lời giải
|
1) Vẽ đồ thị của hàm số \(y = \frac{3}{4}{x^2}\). Tập xác định \(D = \mathbb{R}\). Bảng giá trị:
Đồ thị hàm số \(y = \frac{3}{4}{x^2}\) là Parabol nhận \[Oy\] làm trục đối xứng, có đỉnh \(O\left( {0\,;\,\,0} \right)\), bề lõm hướng lên và đi qua các điểm \(\left( { - 1\,;\,\,\frac{3}{4}} \right),\,\,\left( {1\,;\,\,\frac{3}{4}} \right),\,\)\(\,\left( { - 2\,;\,\,3} \right),\,\,\left( {2\,;\,\,3} \right).\) |
Ta có đồ thị hàm số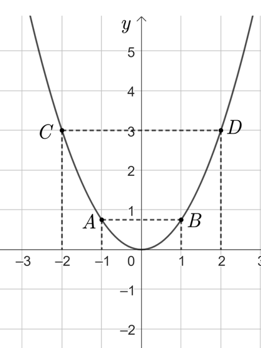 
|
2) Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm của phương trình:
\(\frac{3}{4}{x^2} = x + m\) hay \(\frac{3}{4}{x^2} - x - m = 0\).
Để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt thì phương trình trên phải có hai nghiệm phân biệt
Hay \(\Delta = {( - 1)^2} - 4 \cdot \frac{3}{4}( - m) = 1 + 3m > 0\) hay \(m > \frac{{ - 1}}{3}\).
Vậy với \(m > \frac{{ - 1}}{3}\) thì \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập