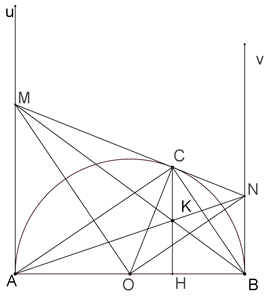
Cho nửa đường tròn tâm \(O\) có đường kính \(AB = 2R.\) Từ \(A\) và \(B\) lần lượt kẻ hai tiếp tuyến \(Au,\,\,Bv\) với nửa đường tròn. Qua một điểm \(C\) thuộc nửa đường tròn (\(C\) khác \(A\) và \(B\)), kẻ tiếp tuyến với nửa đường tròn, nó cắt \(Au\) và \(Bv\) theo thứ tự ở \(M\) và \(N.\)
a) Chứng minh tứ giác \(AMCO\) nội tiếp đường tròn và \(\widehat {CBO} = \widehat {CNO}.\)
b) Kẻ \(CH\) vuông góc với \(AB\) tại \(H,\) gọi \(K\) là giao điểm của \(CH\) với \(AN.\) Chứng minh ba điểm\(M,\,K,\,B\) thẳng hàng.
c) Gọi \(S\) là diện tích của tam giác \(ABC,\)\({S_1}\) là diện tích của tam giác \(MON.\) Hãy tính tỉ số \(\frac{{{S_1}}}{S}\) khi \(AM = 1,5\,R.\)
Cho nửa đường tròn tâm \(O\) có đường kính \(AB = 2R.\) Từ \(A\) và \(B\) lần lượt kẻ hai tiếp tuyến \(Au,\,\,Bv\) với nửa đường tròn. Qua một điểm \(C\) thuộc nửa đường tròn (\(C\) khác \(A\) và \(B\)), kẻ tiếp tuyến với nửa đường tròn, nó cắt \(Au\) và \(Bv\) theo thứ tự ở \(M\) và \(N.\)
a) Chứng minh tứ giác \(AMCO\) nội tiếp đường tròn và \(\widehat {CBO} = \widehat {CNO}.\)
b) Kẻ \(CH\) vuông góc với \(AB\) tại \(H,\) gọi \(K\) là giao điểm của \(CH\) với \(AN.\) Chứng minh ba điểm\(M,\,K,\,B\) thẳng hàng.
c) Gọi \(S\) là diện tích của tam giác \(ABC,\)\({S_1}\) là diện tích của tam giác \(MON.\) Hãy tính tỉ số \(\frac{{{S_1}}}{S}\) khi \(AM = 1,5\,R.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a) Tứ giác \(AMCO\) có : \(\widehat {MAO} = {90^{\rm{o}}};\) \(\widehat {MCO} = {90^{\rm{o}}}\) |
|
\(\widehat {MAO} + \widehat {MCO} = {180^{\rm{o}}}\) Vậy tứ giác \(AMCO\) nội tiếp đường tròn. |
|
Tương tự ta có tứ giác \(COBN\) nội tiếp |
|
\( \Rightarrow \widehat {CBO} = \widehat {CNO}\)
|
|
b)Ta có: \(CK//AM\) nên \(\frac{{KN}}{{KA}} = \frac{{CN}}{{CM}}\) |
|
Mà \(MC = MA,\,\,NC = NB\) nên \(\frac{{KN}}{{KA}} = \frac{{NB}}{{MA}}\,\,\left( 1 \right)\) |
|
Ta lại có\(\widehat {MAK} = \widehat {ANB}\) (so le trong) (2) Từ (1) và (2) ta được \(\Delta AKM\)ഗ\(\Delta NKB\) |
|
\( \Rightarrow \widehat {AKM} = \widehat {NKB}\) Mà \(A,\,K,\,N\) thẳng hàng nên \(M,\,K,\,B\) thẳng hàng (đpcm). |
|
c) Ta có \(\Delta MON\)ഗ\(\Delta ACB\) nên tam giác \(MON\) vuông tại O, cho ta: \(O{C^2} = CM.CN \Rightarrow CN = \frac{2}{3}R\) ; \(MN = MC + CN = \frac{{13}}{6}R\) |
|
\(\frac{{{S_1}}}{S} = {\left( {\frac{{MN}}{{AB}}} \right)^2} = \frac{{169}}{{144}}.\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) Nhân dịp kỉ niệm 10 năm thành lập, cửa hàng GNH có thực hiện chương trình giảm giá cho mặt hàng X là \(20\% \) và mặt hàng Y là \(15\% \) so với giá niêm yết. Bà Giới mua 2 món hàng X và 1 món hàng Y phải trả số tiền là \(395000\) đồng. Ngày cuối cùng của chương trình, cửa hàng thay đổi bằng cách giảm giá mặt hàng X là \(30\% \) và mặt hàng Y là \(25\% .\) Vào ngày hôm đó, cô Định mua 3 món hàng X và 2 món hàng Y thì trả số tiền là \(603000\) đồng. Tính giá niêm yết của mỗi món hàng X và Y (giá niêm yết là giá ghi trên món hàng nhưng chưa thực hiện giảm giá).
b) Tìm tất cả các giá trị của tham số \[m\] để phương trình \[{x^2} - \left( {2m - 1} \right)x + {m^2} - 7 = 0\] có hai nghiệm phân biệt \[{x_1},{x_2}\] thoả mãn điều kiện \[4{x_1} + 3{x_2} = 1.\]
a) Nhân dịp kỉ niệm 10 năm thành lập, cửa hàng GNH có thực hiện chương trình giảm giá cho mặt hàng X là \(20\% \) và mặt hàng Y là \(15\% \) so với giá niêm yết. Bà Giới mua 2 món hàng X và 1 món hàng Y phải trả số tiền là \(395000\) đồng. Ngày cuối cùng của chương trình, cửa hàng thay đổi bằng cách giảm giá mặt hàng X là \(30\% \) và mặt hàng Y là \(25\% .\) Vào ngày hôm đó, cô Định mua 3 món hàng X và 2 món hàng Y thì trả số tiền là \(603000\) đồng. Tính giá niêm yết của mỗi món hàng X và Y (giá niêm yết là giá ghi trên món hàng nhưng chưa thực hiện giảm giá).
b) Tìm tất cả các giá trị của tham số \[m\] để phương trình \[{x^2} - \left( {2m - 1} \right)x + {m^2} - 7 = 0\] có hai nghiệm phân biệt \[{x_1},{x_2}\] thoả mãn điều kiện \[4{x_1} + 3{x_2} = 1.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Gọi giá niêm yết của mặt hàng X và Y lần lượt là \[x,y\] (đồng) |
|
Lập được hệ phương trình \[\left\{ \begin{array}{l}2x\left( {1 - 20\% } \right) + y\left( {1 - 15\% } \right)\,\,\,\, = 395000\\3x\left( {1 - 30\% } \right) + 2y\left( {1 - 25\% } \right) = 603000\end{array} \right.\] |
|
Giải được \[\left\{ \begin{array}{l}x = 130000\\y = 220000\end{array} \right.\,\] |
|
Kết luận đúng. |
|
b)Ta có \(\Delta = - 4m + 29\) Để phương trình có hai nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow m < \frac{{29}}{4}\) |
|
Theo hệ thức Vi-ét ta có : \[{x_1} + {x_2} = 2m - 1\]; \[\,{x_1}.{x_2} = {m^2} - 7\] |
|
Ta có : \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 1\\4{x_1} + 3{x_2} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_1} = 4 - 6m\\{x_2} = 8m - 5\end{array} \right.\] |
|
\[{x_1}.{x_2} = {m^2} - 7 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \frac{{13}}{{49}}\end{array} \right.\] (nhận). |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Chia được thành các tổ hợp số: \(\left( {1\,;\,1\,;\,1\,;6} \right),\,\,\left( {2\,;\,2\,;\,2\,;3} \right),\,\,\left( {1\,;\,1\,;\,2\,;5} \right),\,\left( {1\,;\,1\,;\,3\,;4} \right),\,\left( {2\,;\,2\,;\,1\,;4} \right),\,\left( {3\,;\,3\,;\,1\,;2} \right)\) |
|
Có 4 cách để thử mỗi tổ hợp số \(\left( {1\,;\,1\,;\,1\,;6} \right),\,\,\left( {2\,;\,2\,;\,2\,;3} \right)\) |
|
Có 12 cách để thử mỗi tổ hợp số \(\left( {1\,;\,1\,;\,2\,;5} \right),\,\left( {1\,;\,1\,;\,3\,;4} \right),\,\left( {2\,;\,2\,;\,1\,;4} \right),\,\left( {3\,;\,3\,;\,1\,;2} \right)\) |
|
Vậy ông Tuệ phải thực hiện tối đa \(2.4 + 4.12 = 56\) lần |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập