Cho \(a \ge 0,\,b \ge 0\) thỏa mãn \(2a + 3b \le 6\) và \(2a + b \le 4.\) Chứng minh rằng:
\( - \frac{{22}}{9} \le {a^2} - 2a - b \le 0.\)
Cho \(a \ge 0,\,b \ge 0\) thỏa mãn \(2a + 3b \le 6\) và \(2a + b \le 4.\) Chứng minh rằng:
\( - \frac{{22}}{9} \le {a^2} - 2a - b \le 0.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
\(2a + 3b \le 6 \Rightarrow - \,b \ge \frac{2}{3}a - 2\) |
|
\({a^2} - 2a - b \ge {a^2} - 2a + \frac{2}{3}a - 2 = {\left( {a - \frac{2}{3}} \right)^2} - \frac{{22}}{9} \ge - \frac{{22}}{9}\,\,\left( 1 \right)\) |
|
\(2a + b \le 4 \Rightarrow 2{a^2} + ab \le 4a\) |
|
\( \Rightarrow {a^2} - 2a - b \le - \frac{{ab}}{2} - b \le 0\,\,\left( 2 \right)\) Từ (1) và (2) suy ra điều phải chứng minh.
|
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
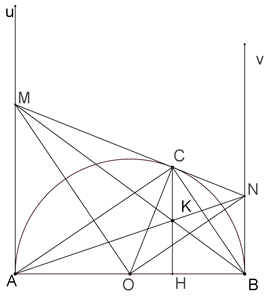
a) Tứ giác \(AMCO\) có : \(\widehat {MAO} = {90^{\rm{o}}};\) \(\widehat {MCO} = {90^{\rm{o}}}\) |
|
\(\widehat {MAO} + \widehat {MCO} = {180^{\rm{o}}}\) Vậy tứ giác \(AMCO\) nội tiếp đường tròn. |
|
Tương tự ta có tứ giác \(COBN\) nội tiếp |
|
\( \Rightarrow \widehat {CBO} = \widehat {CNO}\)
|
|
b)Ta có: \(CK//AM\) nên \(\frac{{KN}}{{KA}} = \frac{{CN}}{{CM}}\) |
|
Mà \(MC = MA,\,\,NC = NB\) nên \(\frac{{KN}}{{KA}} = \frac{{NB}}{{MA}}\,\,\left( 1 \right)\) |
|
Ta lại có\(\widehat {MAK} = \widehat {ANB}\) (so le trong) (2) Từ (1) và (2) ta được \(\Delta AKM\)ഗ\(\Delta NKB\) |
|
\( \Rightarrow \widehat {AKM} = \widehat {NKB}\) Mà \(A,\,K,\,N\) thẳng hàng nên \(M,\,K,\,B\) thẳng hàng (đpcm). |
|
c) Ta có \(\Delta MON\)ഗ\(\Delta ACB\) nên tam giác \(MON\) vuông tại O, cho ta: \(O{C^2} = CM.CN \Rightarrow CN = \frac{2}{3}R\) ; \(MN = MC + CN = \frac{{13}}{6}R\) |
|
\(\frac{{{S_1}}}{S} = {\left( {\frac{{MN}}{{AB}}} \right)^2} = \frac{{169}}{{144}}.\) |
Câu 2
a) Nhân dịp kỉ niệm 10 năm thành lập, cửa hàng GNH có thực hiện chương trình giảm giá cho mặt hàng X là \(20\% \) và mặt hàng Y là \(15\% \) so với giá niêm yết. Bà Giới mua 2 món hàng X và 1 món hàng Y phải trả số tiền là \(395000\) đồng. Ngày cuối cùng của chương trình, cửa hàng thay đổi bằng cách giảm giá mặt hàng X là \(30\% \) và mặt hàng Y là \(25\% .\) Vào ngày hôm đó, cô Định mua 3 món hàng X và 2 món hàng Y thì trả số tiền là \(603000\) đồng. Tính giá niêm yết của mỗi món hàng X và Y (giá niêm yết là giá ghi trên món hàng nhưng chưa thực hiện giảm giá).
b) Tìm tất cả các giá trị của tham số \[m\] để phương trình \[{x^2} - \left( {2m - 1} \right)x + {m^2} - 7 = 0\] có hai nghiệm phân biệt \[{x_1},{x_2}\] thoả mãn điều kiện \[4{x_1} + 3{x_2} = 1.\]
a) Nhân dịp kỉ niệm 10 năm thành lập, cửa hàng GNH có thực hiện chương trình giảm giá cho mặt hàng X là \(20\% \) và mặt hàng Y là \(15\% \) so với giá niêm yết. Bà Giới mua 2 món hàng X và 1 món hàng Y phải trả số tiền là \(395000\) đồng. Ngày cuối cùng của chương trình, cửa hàng thay đổi bằng cách giảm giá mặt hàng X là \(30\% \) và mặt hàng Y là \(25\% .\) Vào ngày hôm đó, cô Định mua 3 món hàng X và 2 món hàng Y thì trả số tiền là \(603000\) đồng. Tính giá niêm yết của mỗi món hàng X và Y (giá niêm yết là giá ghi trên món hàng nhưng chưa thực hiện giảm giá).
b) Tìm tất cả các giá trị của tham số \[m\] để phương trình \[{x^2} - \left( {2m - 1} \right)x + {m^2} - 7 = 0\] có hai nghiệm phân biệt \[{x_1},{x_2}\] thoả mãn điều kiện \[4{x_1} + 3{x_2} = 1.\]
Lời giải
|
a) Gọi giá niêm yết của mặt hàng X và Y lần lượt là \[x,y\] (đồng) |
|
Lập được hệ phương trình \[\left\{ \begin{array}{l}2x\left( {1 - 20\% } \right) + y\left( {1 - 15\% } \right)\,\,\,\, = 395000\\3x\left( {1 - 30\% } \right) + 2y\left( {1 - 25\% } \right) = 603000\end{array} \right.\] |
|
Giải được \[\left\{ \begin{array}{l}x = 130000\\y = 220000\end{array} \right.\,\] |
|
Kết luận đúng. |
|
b)Ta có \(\Delta = - 4m + 29\) Để phương trình có hai nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow m < \frac{{29}}{4}\) |
|
Theo hệ thức Vi-ét ta có : \[{x_1} + {x_2} = 2m - 1\]; \[\,{x_1}.{x_2} = {m^2} - 7\] |
|
Ta có : \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2m - 1\\4{x_1} + 3{x_2} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_1} = 4 - 6m\\{x_2} = 8m - 5\end{array} \right.\] |
|
\[{x_1}.{x_2} = {m^2} - 7 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \frac{{13}}{{49}}\end{array} \right.\] (nhận). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập