Trong một kì thi có \(60\% \) thí sinh đỗ. Hai bạn A, B cùng dự kì thi đó. Xác suất để chỉ có một bạn thi đỗ là        

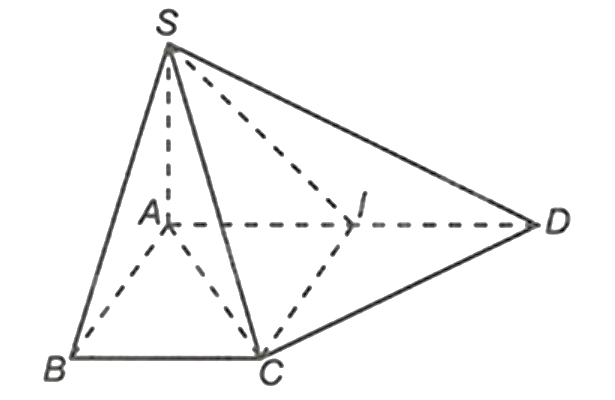
Gọi \(I\) là trung điểm của \(AD\). Suy ra \(AI = ID = \frac{1}{2}AD = a\).

Ta có \(AI = BC\,\,\left( { = a} \right)\) và \(AI\,{\rm{//}}\,BC\,\,\left( {{\rm{do}}\,AD\,{\rm{//}}\,BC} \right)\) nên tứ giác \(ABCI\) là hình bình hành. Lại có \(AI = AB = a\) nên \(ABCI\) là hình thoi, mà \(\widehat {ABC} = 90^\circ \), do đó \(ABCI\) là hình vuông. Khi đó, \(\widehat {AIC} = 90^\circ \), suy ra \(\widehat {CID} = 90^\circ \).

Tam giác \(ICD\) có \(ID = IC = a\) và \(\widehat {CID} = 90^\circ \) nên tam giác \(ICD\) vuông cân tại \(I\).

Suy ra \(\widehat {ICD} = 45^\circ \).

Lại có \(\widehat {ACI} = \frac{1}{2}\widehat {BCI} = \frac{1}{2} \cdot 90^\circ  = 45^\circ \) (vì \(ABCI\) là hình vuông).

Nên ta có \(\widehat {ACD} = \widehat {ACI} + \widehat {ICD} = 90^\circ \). Suy ra \(AC \bot CD\).

Mà \[CD \bot SA\,\,\left( {{\rm{do}}\,\,SA \bot \left( {ABCD} \right)} \right)\], từ đó suy ra \(DC \bot \left( {SAC} \right)\).

Đáp án đúng là: D

Ta có \(\frac{{{{\left( {\sqrt[4]{{{a^3} \cdot {b^2}}}} \right)}^4}}}{{\sqrt[3]{{\sqrt {{a^{12}} \cdot {b^6}} }}}} = \frac{{{a^3} \cdot {b^2}}}{{\sqrt[3]{{{{\left( {{a^{12}} \cdot {b^6}} \right)}^{\frac{1}{2}}}}}}} = \frac{{{a^3} \cdot {b^2}}}{{\sqrt[3]{{{a^6} \cdot {b^3}}}}} = \frac{{{a^3} \cdot {b^2}}}{{{{\left( {{a^6} \cdot {b^3}} \right)}^{\frac{1}{3}}}}} = \frac{{{a^3} \cdot {b^2}}}{{{a^2} \cdot b}} = ab\).