Góc tạo bởi hai đường thẳng \({d_1}:2x + 2\sqrt 3 y + 5 = 0\) và \({d_2}:y - 6 = 0\) bằng
Quảng cáo
Trả lời:
Đáp án đúng là: D
Gọi \(\varphi \) là góc giữa hai đường thẳng đã cho.
Đường thẳng \({d_1}:2x + 2\sqrt 3 y + 5 = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {2;\,2\sqrt 3 } \right)\).
Đường thẳng \({d_2}:y - 6 = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {0;\,\,1} \right)\).
Ta có: \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_1}} } \right|}} = \frac{{\left| {2.0 + 2\sqrt 3 .1} \right|}}{{\sqrt {{2^2} + {{\left( {2\sqrt 3 } \right)}^2}} .\sqrt {{0^2} + {1^2}} }} = \frac{{2\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{2}\). Vậy \(\varphi = 30^\circ \).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
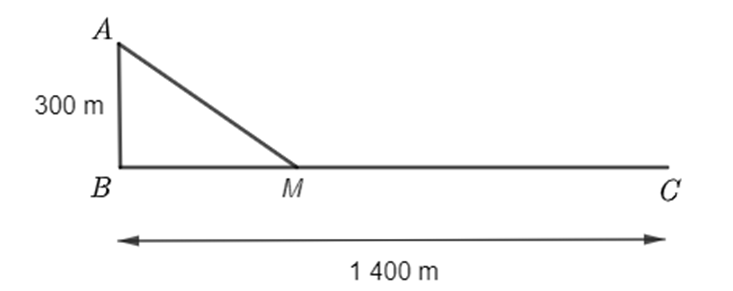
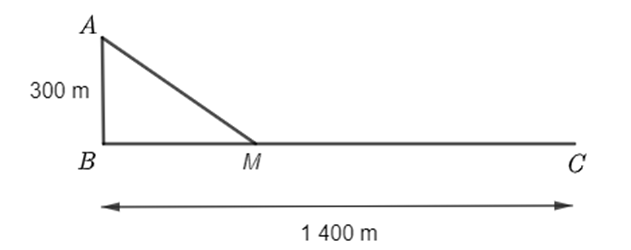
Đổi: 300 m = 0,3 km; 1 400 m = 1,4 km; 20 phút = \(\frac{1}{3}\) giờ.
Đặt \(BM = x\) (km, \(x > 0\)).
Áp dụng định lí Pythagore trong tam giác vuông \(ABM\), ta suy ra \(AM = \sqrt {{{0,3}^2} + {x^2}} \) (km).
Thời gian người đó chèo thuyền từ \(A\) đến \(M\) là \(\frac{{\sqrt {{{0,3}^2} + {x^2}} }}{3}\) (giờ).
Ta có: \(BM + MC = BC \Rightarrow MC = BC - BM = 1,4 - x\) (km).
Thời gian người đó đi bộ từ \(M\) đến \(C\) là \(\frac{{1,4 - x}}{6}\) (giờ).
Khi đó ta có: \(\frac{{\sqrt {{{0,3}^2} + {x^2}} }}{3} + \frac{{1,4 - x}}{6} = \frac{1}{3}\)\( \Leftrightarrow 2\sqrt {0,09 + {x^2}} = x + 0,6\).
Giải phương trình trên ta suy ra được \(x = 0,4\) là giá trị thỏa mãn \(x > 0\).
Vậy \(BM = 0,4\) km = 400 m.
Lời giải
Đáp án đúng là: B
Xét tam thức \(f\left( x \right) = 2{x^2} - 3x - 15\) có hai nghiệm là \({x_1} = \frac{{3 - \sqrt {129} }}{4}\), \({x_2} = \frac{{3 + \sqrt {129} }}{4}\).
Mặt khác có hệ số \(a = 2 > 0\), do đó ta có bảng xét dấu sau:
|
\(x\) |
\( - \infty \) \(\frac{{3 - \sqrt {129} }}{4}\) \(\frac{{3 + \sqrt {129} }}{4}\) \( + \infty \) |
|
\(f\left( x \right)\) |
+ 0 – 0 + |
Dựa vào bảng xét dấu, ta thấy \(f\left( x \right) = 2{x^2} - 3x - 15 \le 0\)\( \Leftrightarrow x \in \left[ {\frac{{3 - \sqrt {129} }}{4};\,\,\frac{{3 + \sqrt {129} }}{4}} \right]\).
Do đó, bất phương trình đã cho có 6 nghiệm nguyên là – 2; – 1; 0; 1; 2; 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Phương trình vô nghiệm;
B. Phương trình có một nghiệm;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ sau:
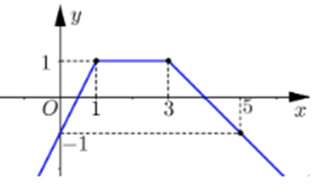
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.