Một chiếc thuyền đang neo đậu tại vị trí A cách bờ biển một khoảng cách AB = 300 m. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 1 400 m. Người ta muốn đưa thuyền vào sát bờ để sửa chữa, người đó có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 6 km/h để tiện lấy dụng cụ sửa chữa tại kho (như hình vẽ dưới). Tính khoảng cách từ vị trí B đến M, biết thời gian người đó đi từ A đến C là 20 phút (giả sử vận tốc dòng nước không đáng kể).
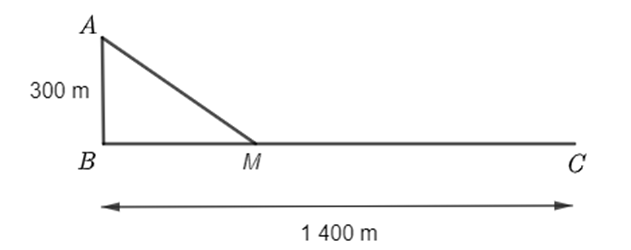
Một chiếc thuyền đang neo đậu tại vị trí A cách bờ biển một khoảng cách AB = 300 m. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 1 400 m. Người ta muốn đưa thuyền vào sát bờ để sửa chữa, người đó có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 6 km/h để tiện lấy dụng cụ sửa chữa tại kho (như hình vẽ dưới). Tính khoảng cách từ vị trí B đến M, biết thời gian người đó đi từ A đến C là 20 phút (giả sử vận tốc dòng nước không đáng kể).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 10 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
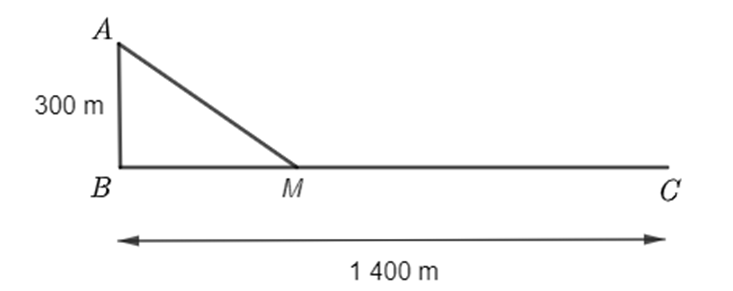
Đổi: 300 m = 0,3 km; 1 400 m = 1,4 km; 20 phút = \(\frac{1}{3}\) giờ.
Đặt \(BM = x\) (km, \(x > 0\)).
Áp dụng định lí Pythagore trong tam giác vuông \(ABM\), ta suy ra \(AM = \sqrt {{{0,3}^2} + {x^2}} \) (km).
Thời gian người đó chèo thuyền từ \(A\) đến \(M\) là \(\frac{{\sqrt {{{0,3}^2} + {x^2}} }}{3}\) (giờ).
Ta có: \(BM + MC = BC \Rightarrow MC = BC - BM = 1,4 - x\) (km).
Thời gian người đó đi bộ từ \(M\) đến \(C\) là \(\frac{{1,4 - x}}{6}\) (giờ).
Khi đó ta có: \(\frac{{\sqrt {{{0,3}^2} + {x^2}} }}{3} + \frac{{1,4 - x}}{6} = \frac{1}{3}\)\( \Leftrightarrow 2\sqrt {0,09 + {x^2}} = x + 0,6\).
Giải phương trình trên ta suy ra được \(x = 0,4\) là giá trị thỏa mãn \(x > 0\).
Vậy \(BM = 0,4\) km = 400 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Giả sử \[A\left( {a;0} \right),\,\,B\left( {0;b} \right)\]
Vì \[OA = OB\] nên \[\left| a \right| = \left| b \right| \Leftrightarrow a = \pm b\]
Phương trình \[AB:\frac{x}{a} + \frac{y}{b} = 1\]
Vì \[M\left( { - 2; - 4} \right) \in AB\] nên \[ - \frac{2}{a} - \frac{4}{b} = 1 & \left( * \right)\]
Nếu \[a = b\] thì \[\left( * \right) \Leftrightarrow - \frac{6}{a} = 1 \Rightarrow a = b = - 6\]
Vậy phương trình \[AB:\frac{x}{{ - 6}} + \frac{y}{{ - 6}} = 1 \Leftrightarrow x + y + 6 = 0\]
Nếu \[a = - b\] thì \[\left( * \right) \Leftrightarrow - \frac{2}{a} + \frac{4}{a} = 1 \Rightarrow \frac{2}{a} = 1 \Rightarrow a = 2 \Rightarrow b = - 2\]
Vậy phương trình \[AB:\frac{x}{2} - \frac{y}{2} = 1 \Leftrightarrow x - y - 2 = 0\].
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Hàm số \(y = {x^2} + 2mx + 5\) có \(a = 1 > 0\) nên hàm số đạt giá trị nhỏ nhất khi \(x = - \frac{b}{{2a}} = - \frac{{2m}}{{2.1}} = - m\).
Theo bài ra ta có: \(y\left( { - m} \right) = 1 \Leftrightarrow {\left( { - m} \right)^2} + 2m.\left( { - m} \right) + 5 = 1 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập