Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điền mẫu áo đó theo thang điểm là 100. Kết quả được ghi lại trong bảng dưới.
|
Điểm |
\[\left[ {50,60} \right)\] |
\(\left[ {60;70} \right)\) |
\(\left[ {70;80} \right)\) |
\(\left[ {80;90} \right)\) |
\(\left[ {90;100} \right)\) |
|
Tần số |
4 |
5 |
23 |
6 |
2 |
Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau đây?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 11 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Cỡ mẫu \(n = 4 + 5 + 23 + 6 + 2 = 40.\)
Gọi \({x_1},...,{x_{40}}\) là điểm mà 40 người đó cho mẫu áo sơ mi đang khảo sát theo thang điểm 100 và giả sử dãy này đã được sắp xếp theo thứ tự không giảm.
Khi đó: \({x_1},...,{x_4}\) thuộc nhóm \[\left[ {50,60} \right);\]
\({x_5},...,{x_9}\) thuộc nhóm \(\left[ {60;70} \right);\)
\({x_{10}},...,{x_{32}}\) thuộc nhóm \(\left[ {70;80} \right);\)
\({x_{33}},...,{x_{38}}\) thuộc nhóm \(\left[ {80;90} \right);\)
\({x_{39}},\,\,{x_{49}}\) thuộc nhóm \(\left[ {90;100} \right).\)
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{10}} + {x_{11}}}}{2}.\) Do \({x_{10}},\,\,{x_{11}}\) đều thuộc nhóm \(\left[ {70;80} \right)\) nên nhóm này chứa \({Q_1}.\)
Do đó, \(p = 3;\) \({a_3} = 70;\) \({m_3} = 23;\) \({m_2} = 5;\) \({m_1} = 4;\)\({a_4} - {a_3} = 80 - 70 = 10\) và ta có:
\({Q_1} = 70 + \frac{{\frac{{40}}{4} - \left( {5 + 4} \right)}}{{23}}.10 = \frac{{1\,\,620}}{{23}} \approx 70,4.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(P = \frac{{{6^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}} = \frac{{{{\left( {2 \cdot 3} \right)}^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}} = \frac{{{2^{3 + \sqrt 5 }} \cdot {3^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}}\)
\( = {2^{\left( {3 + \sqrt 5 } \right) - \left( {2 + \sqrt 5 } \right)}} \cdot {3^{\left( {3 + \sqrt 5 } \right) - \left( {1 + \sqrt 5 } \right)}} = {2^1} \cdot {3^2} = 18.\)
Lời giải
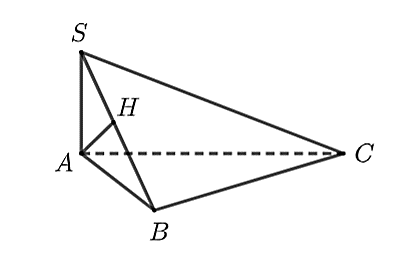
a) Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot BC\).
Lại có \(BC \bot AB\) (do tam giác \(ABC\) vuông tại \(B\)).
Từ đó suy ra \(BC \bot \left( {SAB} \right)\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.