Đo cân nặng của \(40\) học sinh lớp 12B ta được như sau:

Tứ phân vị thứ hai của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào sau đây?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 11 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: C
Giả sử \({x_1};{x_2};...;{x_{40}}\) là cân nặng của 40 học sinh lớp 12B xếp theo thứ tự không giảm.
Có \({x_1};...;{x_4} \in \left[ {40;45} \right)\) ; \({x_5};...;{x_{17}} \in \left[ {45;50} \right)\) ; \({x_{18}};...;{x_{24}} \in \left[ {50;55} \right)\) ; \({x_{25}};...;{x_{29}} \in \left[ {55;60} \right)\) ;
\({x_{30}};...;{x_{35}} \in \left[ {60;65} \right)\) ; \({x_{36}};...;{x_{37}} \in \left[ {65;70} \right)\) ; \({x_{38}} \in \left[ {70;75} \right)\) ; \({x_{39}};{x_{40}} \in \left[ {75;80} \right)\).
Tứ phân vị thứ hai của mẫu số liệu là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right)\) mà \({x_{20}};{x_{21}} \in \left[ {50;55} \right)\).
Khi đó ta có : \(n = 40;{u_m} = 50;C = 17;{n_m} = 7;{u_{m + 1}} = 55\).
Do đó \({Q_2} = 50 + \frac{{\frac{{40}}{2} - 17}}{7} \cdot \left( {55 - 50} \right) \approx 52,14\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: D
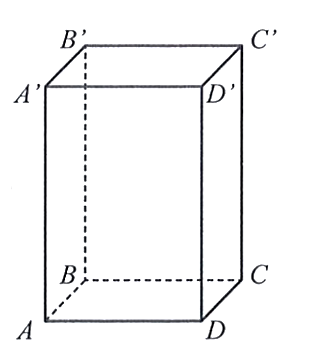
Ta có \(A'D\,{\rm{//}}\,B'C,\,\,B'C \bot BC' \Rightarrow A'D \bot BC'\).
Câu 2
Lời giải
Đáp án đúng là: B
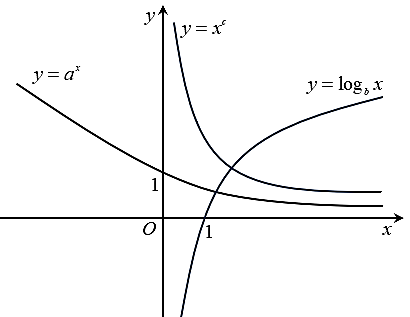
Ta thấy đồ thị \(y = {x^c}\) đi xuống từ trái qua phải nên \(c < 0\), đồ thị \(y = {a^x}\) đi xuống từ trái qua phải nên \(0 < a < 1\), đồ thị \(y = {\log _b}x\) đi lên từ trái qua phải nên \(b > 1.\)
Vậy \(c < 0 < a < 1 < b.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.