(4,0 điểm)
Một thùng lấy nước bằng tôn có dạng hình trụ có chiều cao là \[36cm\] và đường kính đáy là \[3dm\].
a) Tính thể tích của thùng nước đó. (làm tròn đến hàng đơn vị)
b) Người ta sử dụng thùng nước trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}.\)Hỏi cần phải đổ ít nhất bao nhiêu thùng thì mới đầy bể chứa? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.

Một thùng lấy nước bằng tôn có dạng hình trụ có chiều cao là \[36cm\] và đường kính đáy là \[3dm\].
a) Tính thể tích của thùng nước đó. (làm tròn đến hàng đơn vị)
b) Người ta sử dụng thùng nước trên để múc nước đổ vào một bể chứa có dung tích \(1\;{m^3}.\)Hỏi cần phải đổ ít nhất bao nhiêu thùng thì mới đầy bể chứa? Biết rằng mỗi lần xách người ta chỉ đổ đầy \(90{\rm{\% }}\) thùng để nước không đổ ra ngoài.
Quảng cáo
Trả lời:
a) Đổi: 3dm = 30cm; \(R = 30:2 = 15\,\left( {cm} \right)\);
Thể tích của thùng nước là: \(V = \pi {R^2}h\)
\( = \pi {.15^2}.36 = 8100\pi \approx 25447\,\left( {c{m^3}} \right)\)
b) Thể tích nước mỗi lần xách là: \(25447.90\% = 22902,3\left( {c{m^3}} \right) = 0,0229023\left( {{m^3}} \right)\)
Số thùng nước cần đổ để đầy bể là:\(1:0,0229023 \approx 43,66\) (thùng)
Vậy cần phải đổ ít nhất 44 thùng để đầy bể chứa.
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \((O,R)\) và dây \(AB\) cố định (AB không là đường kính). Gọi \(N\) là trung điểm của \(AB.\) Qua \(N,\) kẻ đường kính \(CD\) của đường tròn \((O)\) (\(C\) thuộc cung nhỏ \(AB\)). Lấy điểm \(M\) bất kỳ trên cung lớn \(AB\,\,(M \ne A,M \ne B)\),\(MC\) cắt \(AB\) tại \(F.\) Hai đường thẳng \(DM\) và \(AB\) cắt nhau tại \(E\).
a) Chứng minh bốn điểm \(M,N,C,\,E\) cùng thuộc một đường tròn.
b) Hai đường thẳng \(DF\) và \(CE\) cắt nhau tại \(I\). Chứng minh \(KI.KM = KC.KD\) và \(NE\) là tia phân giác của\(\widehat {MNI}\)
c) Chứng minh rằng: \[\frac{{KC}}{{K{\rm{D}}}} = \frac{{CN}}{{DN}}\]
Cho đường tròn \((O,R)\) và dây \(AB\) cố định (AB không là đường kính). Gọi \(N\) là trung điểm của \(AB.\) Qua \(N,\) kẻ đường kính \(CD\) của đường tròn \((O)\) (\(C\) thuộc cung nhỏ \(AB\)). Lấy điểm \(M\) bất kỳ trên cung lớn \(AB\,\,(M \ne A,M \ne B)\),\(MC\) cắt \(AB\) tại \(F.\) Hai đường thẳng \(DM\) và \(AB\) cắt nhau tại \(E\).
a) Chứng minh bốn điểm \(M,N,C,\,E\) cùng thuộc một đường tròn.
b) Hai đường thẳng \(DF\) và \(CE\) cắt nhau tại \(I\). Chứng minh \(KI.KM = KC.KD\) và \(NE\) là tia phân giác của\(\widehat {MNI}\)
c) Chứng minh rằng: \[\frac{{KC}}{{K{\rm{D}}}} = \frac{{CN}}{{DN}}\]
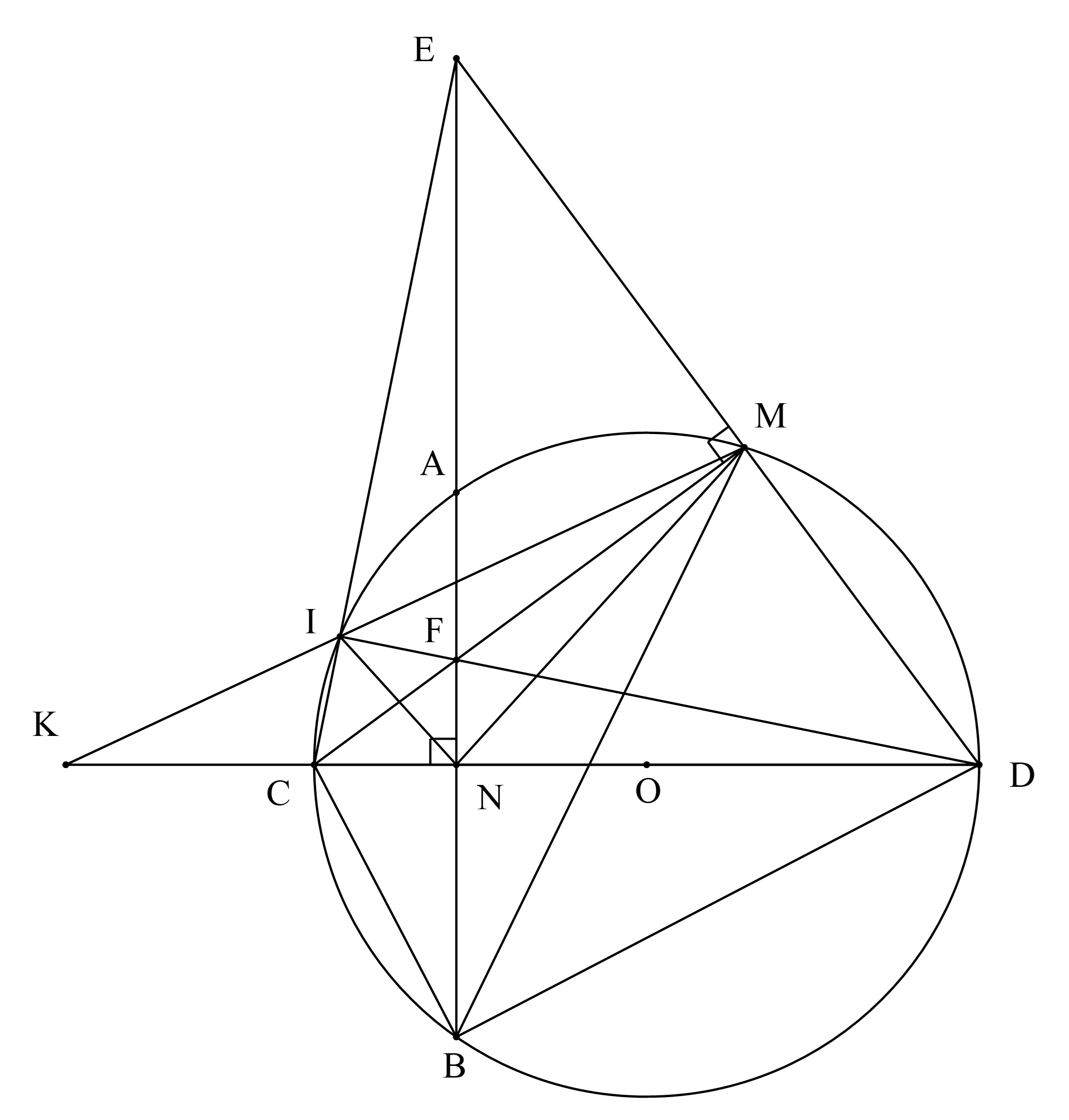
2a) Chứng minh bốn điểm \(M,N,C,\,E\) cùng thuộc một đường tròn
Lập luận \(\widehat {ENC} = 90^\circ \)
Lập luận \(\widehat {EMC} = 90^\circ \)
Suy ra \(\widehat {ENC} = \widehat {EMC} = 90^\circ \)
Suy ra M; N cùng thuộc đường tròn đường kính CE hay 4 điểm M: N; C; E cùng thuộc một đường tròn đường kính CE.
2b) Chứng minh \(KI.KM = KC.KD\) và \(NE\) là tia phân giác của góc \(MNI.\)
Có \(\widehat {KIC}{\rm{ = 18}}{{\rm{0}}^0} - \widehat {CIM}{\rm{ = }}\widehat {CDM}\)( vì tổng các góc đối nhau của tứ giác nội tiếp CIMD bằng 1800)
Xét \(\Delta KIC\) và \(\Delta KDM\) có:
\(\widehat K{\rm{ chung; }}\widehat {KIC} = \widehat {KDM}\) (cmt)
Chứng minh: \(NE\) là tia phân giác của \(\widehat {MNI}\).
Xét \(\Delta CDE\) có: \(CM \bot DE;EN \bot CD\) và \(CM{\rm{ giao }}EN\) tại \(F\)
\[ \Rightarrow F\] là trực tâm \(\Delta CDE\)
\( \Rightarrow DF \bot CE\) tại \(I\) (\(DF\) cắt \(CE\) tại \(I\) ) hay \(DI \bot CE\) tại \(I\).
\( \Rightarrow \widehat {DIC} = 90^\circ \)
\( \Rightarrow I\) thuộc đường tròn tâm \(O\), đường kính \(CD\)
Xét tứ giác \(CIFN\) có:
\[\widehat {CIF} + \widehat {CNF} = 90^\circ + 90^\circ = 180^\circ \]
Mà hai góc đối nhau trong tứ giác
Nên tứ giác \(CIFN\) nội tiếp đường tròn
\( \Rightarrow \widehat {ICF} = \widehat {INF}\) (hai góc nội tiếp cùng chắn )
Chứng minh được tứ giác \[FMDN\] nội tiếp
\( \Rightarrow \widehat {FNM} = \widehat {FDM}\) (hai góc nội tiếp cùng chắn )
Mà \(\widehat {ICM} = \widehat {IDM}\) (góc nội tiếp cùng chắn của đường tròn \((O)\))
Hay \(\widehat {ICF} = \widehat {FDM}\)
\( \Rightarrow \widehat {INF} = \widehat {FNM}\)
\( \Rightarrow NF\) là tia phân giác của \(\widehat {MNI}\)\( \Rightarrow NE\) là tia phân giác của \(\widehat {MNI}\)
2c) Chứng minh rằng: \[\frac{{KC}}{{K{\rm{D}}}} = \frac{{CN}}{{DN}}\]
Chứng minh được
Mà \(\frac{{KC}}{{KM}} = \frac{{CI}}{{DM}}\)( Vì )
nên \[\frac{{KC}}{{K{\rm{D}}}} = \frac{{KC}}{{KM}}.\frac{{KM}}{{KD}} = \frac{{CI}}{{DM}}.\frac{{CM}}{{DI}}\] (1)
Tương tự, \[\frac{{CN}}{{CE}} = \frac{{CI}}{{C{\rm{D}}}}\] và \[\frac{{DN}}{{DE}} = \frac{{DM}}{{C{\rm{D}}}}\]
Do đó, \[\frac{{CN}}{{DN}} = \frac{{CI}}{{DM}}.\frac{{CE}}{{DE}}\] (2)
Chứng minh được \[\frac{{EC}}{{ED}} = \frac{{CM}}{{DI}}\] (3)
Từ (1); (2); (3) suy ra \[\frac{{KC}}{{K{\rm{D}}}} = \frac{{CN}}{{DN}}\]
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số gam thịt bò và thịt heo cần sử dụng lần lượt là \[x;y\left( g \right)\] \[\left( {x > 0;y > 0} \right)\]
\[1\] gam thịt bò có chứa \[80:100 = 0,8\] (đv protein) và \[20:100 = 0,2\] (đv lipit)
\[1\] gam thịt heo có chứa \[60:100 = 0,6\](đv protein) và \[40:100 = 0,4\] (đv lipit)
Do cần đảm bảo đủ \[900\] đơn vị protein nên ta có phương trình: \[0,8x + 0,6y = 900\left( 1 \right)\]
Do cần đảm bảo đủ \[400\] đơn vị lipit nên ta có phương trình: \[0,2x + 0,4y = 400\left( 2 \right)\]
Từ \(\left( 1 \right);\left( 2 \right)\) ta có hệ phương trình \[\left\{ \begin{array}{l}0,8x + 0,6y = 900\\0,2x + 0,4y = 400\end{array} \right.\]\[ \Rightarrow \left\{ \begin{array}{l}x = 600\left( {{\rm{t/m}}} \right)\\y = 700\left( {{\rm{t/m}}} \right)\end{array} \right.\]
Vậy số gam thịt bò và thịt heo người nội trợ cần sử dụng lần lượt là \[600g;\,\,700g.\]
Lời giải
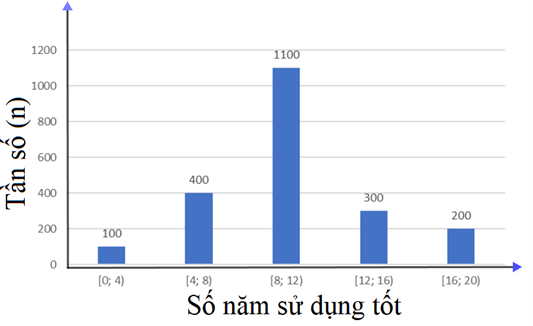
Từ biểu đồ ta có nhóm [8; 12) có tần số ghép nhóm là 1100
(nghĩa là có 1100 xe loại đó được sử dụng tốt từ 8 tới dưới 12 năm mới phải thực hiện đại tu lần đầu trong 4 năm sử dụng tiếp theo)
Tần số tương đối ghép nhóm là \(\frac{{1100}}{{2000}}.100\% = 55\% \)
(nghĩa là có 55% số xe loại đó sử dụng tốt từ 8 tới 12 năm, sau đó các xe này đều phải đại tu, sửa chữa hoặc thay thế trong 4 năm sử dụng tiếp theo.
Câu 3
(1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0\,;\,x \ne 9\)
1) Tính giá trị của biểu thức A khi x = 25.
2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\).
3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\).
(1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0\,;\,x \ne 9\)
1) Tính giá trị của biểu thức A khi x = 25.
2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\).
3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.