(0,5 điểm)
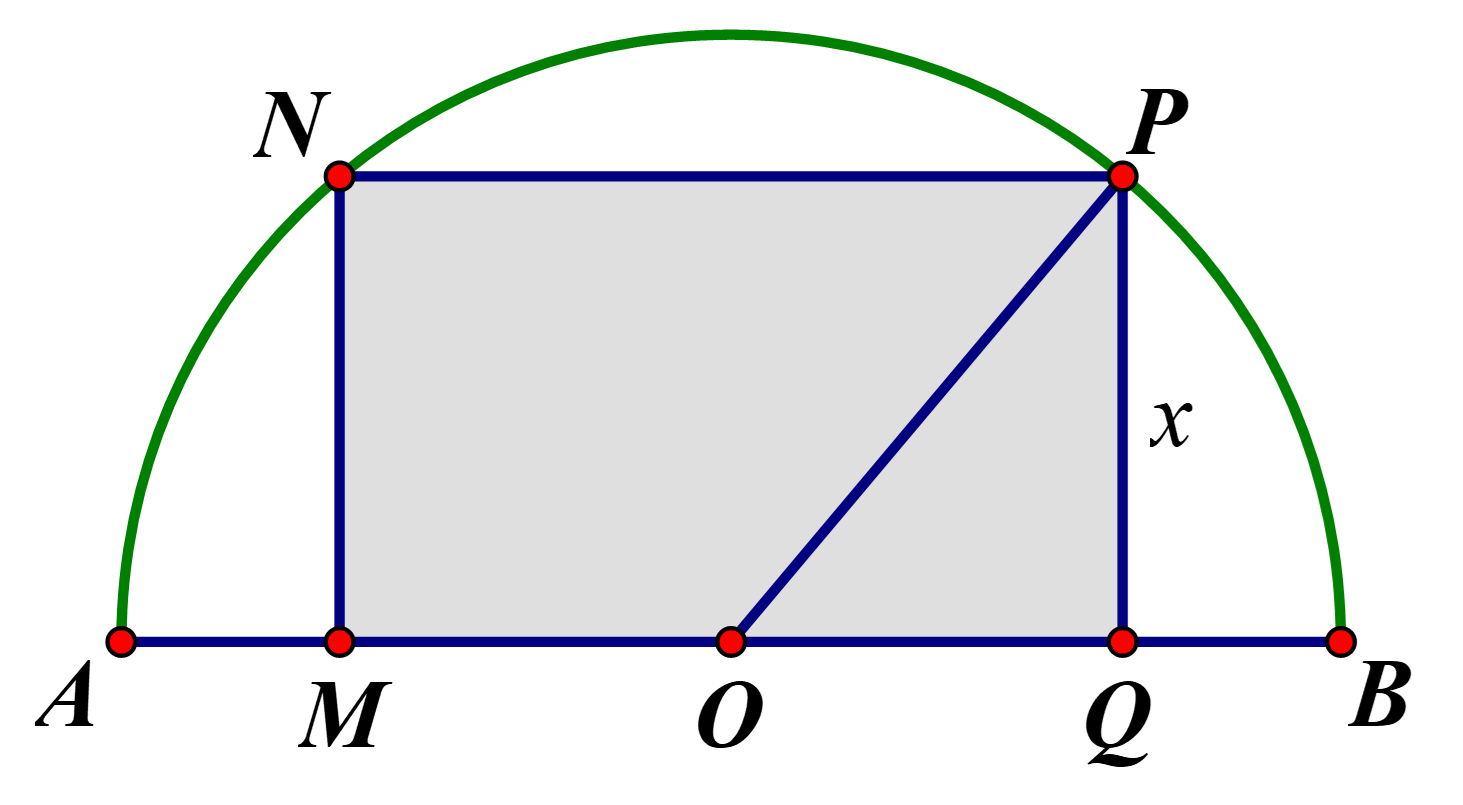
Tìm diện tích lớn nhất của hình chữ nhật \(MNPQ\) nội tiếp trong nửa đường tròn \(\left( O \right)\) bán kính \(10cm,\) biết một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn (như hình vẽ).
(0,5 điểm)
Tìm diện tích lớn nhất của hình chữ nhật \(MNPQ\) nội tiếp trong nửa đường tròn \(\left( O \right)\) bán kính \(10cm,\) biết một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn (như hình vẽ).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(x\left( {cm} \right)\) là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn \(\left( {0 < x < 10} \right)\)
Khi đó độ dài cạnh hình chữ nhật nằm dọc trên đường kính của đường tròn là:
\(MQ = 2\sqrt {{{10}^2} - {x^2}} \left( {cm} \right)\)
Diện tích hình chữ nhật \(MNPQ\) là: \(S = x.2\sqrt {100 - {x^2}} = 2\sqrt {{x^2}.\left( {100 - {x^2}} \right)} \left( {c{m^2}} \right)\)
Ta có: \(2\sqrt {{x^2}.\left( {100 - {x^2}} \right)} \le {x^2} + 100 - {x^2} = 100\).
Dấu bằng xảy ra khi \({x^2} = 100 - {x^2} \Rightarrow x = 5\sqrt 2 \)
Vậy diện tích lớn nhất của hình chữ nhật là \(100c{m^2}\) khi \(x = 5\sqrt 2 \left( {cm} \right)\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số gam thịt bò và thịt heo cần sử dụng lần lượt là \[x;y\left( g \right)\] \[\left( {x > 0;y > 0} \right)\]
\[1\] gam thịt bò có chứa \[80:100 = 0,8\] (đv protein) và \[20:100 = 0,2\] (đv lipit)
\[1\] gam thịt heo có chứa \[60:100 = 0,6\](đv protein) và \[40:100 = 0,4\] (đv lipit)
Do cần đảm bảo đủ \[900\] đơn vị protein nên ta có phương trình: \[0,8x + 0,6y = 900\left( 1 \right)\]
Do cần đảm bảo đủ \[400\] đơn vị lipit nên ta có phương trình: \[0,2x + 0,4y = 400\left( 2 \right)\]
Từ \(\left( 1 \right);\left( 2 \right)\) ta có hệ phương trình \[\left\{ \begin{array}{l}0,8x + 0,6y = 900\\0,2x + 0,4y = 400\end{array} \right.\]\[ \Rightarrow \left\{ \begin{array}{l}x = 600\left( {{\rm{t/m}}} \right)\\y = 700\left( {{\rm{t/m}}} \right)\end{array} \right.\]
Vậy số gam thịt bò và thịt heo người nội trợ cần sử dụng lần lượt là \[600g;\,\,700g.\]
Lời giải
a) Đổi: 3dm = 30cm; \(R = 30:2 = 15\,\left( {cm} \right)\);
Thể tích của thùng nước là: \(V = \pi {R^2}h\)
\( = \pi {.15^2}.36 = 8100\pi \approx 25447\,\left( {c{m^3}} \right)\)
b) Thể tích nước mỗi lần xách là: \(25447.90\% = 22902,3\left( {c{m^3}} \right) = 0,0229023\left( {{m^3}} \right)\)
Số thùng nước cần đổ để đầy bể là:\(1:0,0229023 \approx 43,66\) (thùng)
Vậy cần phải đổ ít nhất 44 thùng để đầy bể chứa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
(1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0\,;\,x \ne 9\)
1) Tính giá trị của biểu thức A khi x = 25.
2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\).
3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\).
(1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0\,;\,x \ne 9\)
1) Tính giá trị của biểu thức A khi x = 25.
2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\).
3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập