(4,0 điểm)
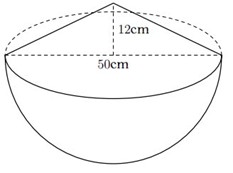
Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần gạo vun lên có dạng hình nón cao \(12cm\).
a) Tính thể tích phần gạo trong thùng.
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là\(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?
Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần gạo vun lên có dạng hình nón cao \(12cm\).
a) Tính thể tích phần gạo trong thùng.
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là\(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?

Quảng cáo
Trả lời:
a) Bán kính của hình cầu là: \(R = \frac{d}{2} = \frac{{50}}{2} = 25{\kern 1pt} {\kern 1pt} \left( {cm} \right)\)
Thể tích phần gạo hình cầu là: \({V_c} = \frac{1}{2} \cdot \frac{4}{3}\pi {R^3} = \frac{1}{2} \cdot \frac{4}{3}\pi {25^3} = \frac{{31{\kern 1pt} 250}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích phần gạo vun lên dạng hình nón là: \({V_n} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi \cdot {25^2} \cdot 12 = 2500\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo trong thùng là: \({V_g} = \frac{{31{\kern 1pt} 250}}{3}\pi + 2500\pi = \frac{{38750}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
b) Thể tích lon là: \(\pi {.5^2}.14 = 350{\kern 1pt} \pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo một ngày múc là : \(4.90\% .350\pi = 1260\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Ta có : \(\frac{{38{\kern 1pt} 750}}{\pi }:1{\kern 1pt} 260\pi \approx 10,3\)
Vậy cần ít nhất 11 ngày để dùng hết số gạo trong thùng.
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn tâm \[(O)\] và dây \[BC\] cố định không đi qua \[O\]. Trên cung lớn \[BC\] lấy điểm \[A\] sao cho \[AB < AC\]. Kẻ đường kính \[AK,E\] là hình chiếu của \[C\] trên \[AK\]. \[M\] là trung điểm của \(BC\).
a) Chứng minh bốn \(C,\,E,\,\,M,\,O\)cùng thuộc một đường tròn.
b) Kẻ \(AD \bot BC\) tại \[D\]. Chứng minh \[AD.AK = AB.AC\] và \[\Delta MDE\] cân.
c) Gọi \[F\] là hình chiếu của \[B\] trên \[AK\]. Chứng minh khi 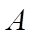 di chuyển trên cung lớn \[BC\] thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
di chuyển trên cung lớn \[BC\] thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
Cho đường tròn tâm \[(O)\] và dây \[BC\] cố định không đi qua \[O\]. Trên cung lớn \[BC\] lấy điểm \[A\] sao cho \[AB < AC\]. Kẻ đường kính \[AK,E\] là hình chiếu của \[C\] trên \[AK\]. \[M\] là trung điểm của \(BC\).
a) Chứng minh bốn \(C,\,E,\,\,M,\,O\)cùng thuộc một đường tròn.
b) Kẻ \(AD \bot BC\) tại \[D\]. Chứng minh \[AD.AK = AB.AC\] và \[\Delta MDE\] cân.
c) Gọi \[F\] là hình chiếu của \[B\] trên \[AK\]. Chứng minh khi di chuyển trên cung lớn \[BC\] thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
a) Chứng minh bốn \(C,\,E,\,\,M,\,O\)cùng thuộc một đường tròn.
cân tại \(O\), \(M\) là trung điểm của \(BC\) nên \(OM\)vừa là đường trung tuyến vừa là đường cao. Suy ra \(OM \bot BC \Rightarrow \widehat {OMC} = 90^\circ \)
Theo bài ra, là hình chiếu của
trên
nên
.
Gọi \(I\) là trung điểm của \[OC\]
Dễ dàng chứng minh \(IO = IE = IM = IC\)
Do đó ,
,
,
cùng thuộc một đường tròn \(\left( I \right)\).
b) *Chứng minh \(AD.AK = AB.AC\)
Xét \(\Delta DBA\) và \(\Delta CK{\rm{A}}\) có
+) \(\widehat {ADB} = \widehat {ACK} = 90^\circ \)
+) \(\widehat {ABD} = \widehat {AKC}\) (Hai góc nội tiếp cùng chắn cung )
Nên
Do đó ta có: \(\frac{{AD}}{{AB}} = \frac{{AC}}{{AK}}\) (cặp cạnh tương ứng tỉ lệ)
Hay \(AD.AK = AB.AC\) (đpcm).
*Chứng minh \(\Delta MDE\) cân.
Theo bài ra \(\left\{ \begin{array}{l}AD \bot BC\\AE \bot EC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat {ADC} = 90^\circ \\\widehat {AEC} = 90^\circ \end{array} \right.\)
Gọi \[Q\] là trung điểm của \(AC\)
Dễ dàng chứng minh \(QA = QC = QD = QE\)
Suy ra bốn điểm \(A,\,C,\,D,\,E\)cùng thuộc đường tròn \(\left( Q \right)\)
Suy ra \(\widehat {CAE} = \widehat {CDE}\) (Hai góc nội tiếp cùng chắn cung \[CE\])
Xét \(\left( O \right)\) ta có: \(\widehat {CBK} = \widehat {CAE}\) (Hai góc nội tiếp cùng chắn cung \[CK\] )
Từ (1) và (2) suy ra mà hai góc này ở vị trí đồng vị (3)
Suy ra
Xét đường tròn \(\left( I \right)\)có: \(\widehat {EMC} = \widehat {EOC}\)(Hai góc nội tiếp cùng chắn ). (4)
Xét đường tròn \(\left( O \right)\)có:\(\widehat {KBC} = \frac{1}{2}\widehat {KOC}\) (Góc nội tiếp và góc ở tâm cùng chắn cung ). (5)
Từ (3); (4) và (5) suy ra: \(\widehat {EMC} = 2\widehat {CDE}\).
\(\Delta MDE\)có \(\widehat {EMC} = \widehat {MDE} + \widehat {MED}\) (góc ngoài của tam giác) mà \(\widehat {EMC} = 2\widehat {MDE}\)
Nên \(\widehat {MDE} = \widehat {MED}\). Do đó, \(\Delta MDE\) cân tại \(M\).
c) Chứng minh khi \(A\) di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
Gọi \(P\) là trung điểm của \(BO\)
Dễ dàng chứng minh được \(PB = PO = PF = PM\)
Suy ra bốn điểm \(O,M,B,F\) cùng thuộc đường tròn \(\left( P \right)\)
Nên \[\widehat {OBM} = \widehat {MFO}\] (Hai góc nội tiếp cùng chắn ).
Xét đường tròn \(\left( I \right)\)có: \[\widehat {MEO} = \widehat {MCO}\] \[CK\] (Hai góc nội tiếp cùng chắn).
Mà \[\widehat {OBM} = \widehat {OCM}\](\[\Delta OCB\]cân tại \[O\].
Do đó \[\widehat {MFO} = \widehat {MEO}\] \[ \Rightarrow \Delta EMF\]cân tại \[M \Rightarrow ME = MF\]
Mà \[ME = MD\] (Tam giác \[MDE\]cân tại \[M\]).
Suy ra:\[MD = ME = ME\].
Suy ra \(M\) là tâm đường tròn ngoại tiếp tam giác \(DEF\).
Mà \(M\) là trung điểm của \(BC\)nên \(M\) là điểm cố định.
Vậy khi \(A\) di chuyển trên cung lớn \(BC\)thì tâm đường tròn ngoại tiếp tam giác \(DEF\)là một điểm cố định.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số học sinh nam và số học sinh nữ của lớp 9A lần lượt là \[x,\,y\] (học sinh; \[x,y\]\[ \in {\mathbb{N}^*}\])
Vì lớp 9A có 35 học sinh nên ta có PT: \[x + y = 35\] (1)
Vì số học sinh không cận thị là 8 nên ta có \[25\% x + 20\% y = 8\](2)
Từ (1) và (2) ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 35\\25\% x + 20\% y = 8\end{array} \right.\]
Tìm ra \[x = 20,\,y = 15\] (TMĐK)
Vậy số học sinh nữ bị cận thị là \[20\% .15 = 3\](học sinh).
Lời giải
Tần số ghép nhóm của nhóm \(\left[ {10;20} \right)\)là \(45\% .40 = 18\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.