(2,5 điểm)
Cận thị trong học sinh ngày càng tăng. Lớp 9A có 35 học sinh, trong đó chỉ có 25% học sinh nam và 20% số học sinh nữ không bị cận thị. Biết tổng số học sinh nam và học sinh nữ không bị cận thị là 8 học sinh. Tính số học sinh nữ không bị cận thị.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 17 !!
Quảng cáo
Trả lời:
Gọi số học sinh nam và số học sinh nữ của lớp 9A lần lượt là \[x,\,y\] (học sinh; \[x,y\]\[ \in {\mathbb{N}^*}\])
Vì lớp 9A có 35 học sinh nên ta có PT: \[x + y = 35\] (1)
Vì số học sinh không cận thị là 8 nên ta có \[25\% x + 20\% y = 8\](2)
Từ (1) và (2) ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 35\\25\% x + 20\% y = 8\end{array} \right.\]
Tìm ra \[x = 20,\,y = 15\] (TMĐK)
Vậy số học sinh nữ bị cận thị là \[20\% .15 = 3\](học sinh).
Câu hỏi cùng đoạn
Câu 2:
Hưởng ứng phong trào trồng cây xanh vì môi trường xanh sạch đẹp. Một chi đoàn dự định trồng 600 cây xanh trong thời gian quy định. Do mỗi ngày họ trồng được nhiều hơn dự định 30 cây nên công việc được hoàn thành sớm hơn quy định 1 ngày. Tính số ngày chi đoàn dự kiến hoàn thành công việc ?
Gọi \[x\] là số ngày dự định để chi đoàn hoàn thành công việc (\[x > 1\]) (ngày)
Số cây dự kiến trồng trong 1 ngày là \[\frac{{600}}{x}\](cây)
Số ngày thực tế để chi đoàn hoàn thành công việc là \[x - 1\](ngày)
Số cây thực tế trồng được trong 1 ngày là \[\frac{{600}}{x} + 30\](cây)
Theo đề bài ta có phương trình:
\[\left( {x - 1} \right)\left( {\frac{{600}}{x} + 30} \right) = 600\]
\[\left( {x - 1} \right)\left( {600 + 30x} \right) = 600x\]
\[600x - 600 + 30{x^2} - 30x = 600x\]
\[30x{}^2 - 30x - 600 = 0\]
\[{x^2} - x - 20 = 0\]
\[{x^2} - 5x + 4x - 20 = 0\]
\[x\left( {x - 5} \right) + 4\left( {x - 5} \right) = 0\]
\[\left( {x - 5} \right)\left( {x + 4} \right) = 0\]
TH1:
\[\begin{array}{l}x - 5 = 0\\x = 5\,\,\,(tm)\end{array}\]
TH2:
\[x + 4 = 0\]
\[x = - 4\,\,(ko\,\,tm)\]
Vậy số ngày dự định để chi đoàn hoàn thành công việc là \[5\]ngày
Câu 3:
Cho phương trình \(3{x^2} + 5x - 6 = 0\) có hai nghiệm \({x_1},{\kern 1pt} {x_2}\).
Không giải phương trình, tính: \(P = \frac{{2{x_2}^2}}{{{x_1} + {x_2}}} + 2{x_1}\).
Cho phương trình \(3{x^2} + 5x - 6 = 0\) có hai nghiệm \({x_1},{\kern 1pt} {x_2}\).
Không giải phương trình, tính: \(P = \frac{{2{x_2}^2}}{{{x_1} + {x_2}}} + 2{x_1}\).
Chứng minh PT có 2 nghiệm phân biệt \[{x_1},\,{x_2}\]
Theo định lý Viet ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - 5}}{3}\\{x_1}{x_2} = - 2\end{array} \right.\]
Theo đề bài ta có :
\[\frac{{2{x_2}^2}}{{{x_1} + {x_2}}} + 2{x_1} = \frac{{2{x_2}^2 + 2{x_1}^2 + 2{x_1}{x_2}}}{{{x_1} + {x_2}}} = \frac{{2\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] + 2{x_1}{x_2}}}{{{x_1} + {x_2}}}\]
\[ = \,\,\frac{{ - 86}}{{15}}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tần số ghép nhóm của nhóm \(\left[ {10;20} \right)\)là \(45\% .40 = 18\).
Lời giải
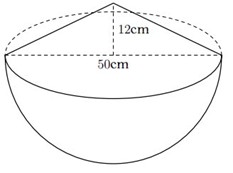
a) Bán kính của hình cầu là: \(R = \frac{d}{2} = \frac{{50}}{2} = 25{\kern 1pt} {\kern 1pt} \left( {cm} \right)\)
Thể tích phần gạo hình cầu là: \({V_c} = \frac{1}{2} \cdot \frac{4}{3}\pi {R^3} = \frac{1}{2} \cdot \frac{4}{3}\pi {25^3} = \frac{{31{\kern 1pt} 250}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích phần gạo vun lên dạng hình nón là: \({V_n} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi \cdot {25^2} \cdot 12 = 2500\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo trong thùng là: \({V_g} = \frac{{31{\kern 1pt} 250}}{3}\pi + 2500\pi = \frac{{38750}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
b) Thể tích lon là: \(\pi {.5^2}.14 = 350{\kern 1pt} \pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Thể tích gạo một ngày múc là : \(4.90\% .350\pi = 1260\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)
Ta có : \(\frac{{38{\kern 1pt} 750}}{\pi }:1{\kern 1pt} 260\pi \approx 10,3\)
Vậy cần ít nhất 11 ngày để dùng hết số gạo trong thùng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.