(1,5 điểm) Cho hai biểu thức \(A = \frac{{\sqrt x + 4}}{{\sqrt x }}\) và \(B = \frac{2}{{\sqrt x + 2}} + \frac{{x + 4}}{{x - 4}}\) với \(x > 0, x \ne 4.\)
1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
2) Rút gọn biểu thức \(B.\)
3) Cho \(P = A. B\). Tìm giá trị của \(x\) khi \(\left| {\,P\,} \right| = P.\)
(1,5 điểm) Cho hai biểu thức \(A = \frac{{\sqrt x + 4}}{{\sqrt x }}\) và \(B = \frac{2}{{\sqrt x + 2}} + \frac{{x + 4}}{{x - 4}}\) với \(x > 0, x \ne 4.\)
1) Tính giá trị của biểu thức \(A\) khi \(x = 9.\)
2) Rút gọn biểu thức \(B.\)
3) Cho \(P = A. B\). Tìm giá trị của \(x\) khi \(\left| {\,P\,} \right| = P.\)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 18 !!
Quảng cáo
Trả lời:
1) Khi \(x = 9\) thì \(A = \frac{{\sqrt x + 4}}{{\sqrt x }} = \frac{{\sqrt 9 + 4}}{{\sqrt 9 }} = \frac{{3 + 4}}{3} = \frac{7}{3}.\)
2) \(B = \frac{2}{{\sqrt x + 2}} + \frac{{x + 4}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{{2\sqrt x - 4 + x + 4}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{{2\sqrt x + x}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}\)
\( = \frac{{\sqrt x \left( {2 + \sqrt x } \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{{\sqrt x }}{{\sqrt x - 2}}\)
3) \(P = A. B = \frac{{\sqrt x + 4}}{{\sqrt x }}.\frac{{\sqrt x }}{{\sqrt x - 2}} = \frac{{\sqrt x + 4}}{{\sqrt x - 2}}\) mà \(\left| {\,P\,} \right| = P\) khi và chỉ khi \(P \ge 0\) hay \(\frac{{\sqrt x + 4}}{{\sqrt x - 2}} \ge 0\) do đó
\[\begin{array}{l}\sqrt x - 2 > 0\\\sqrt x > 2\\x > 4\,\,\,\left( {TM} \right)\end{array}\]
Vậy \(x > 4.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo công thức lãi kép, số tiền cả vốn lẫn lãi nhận được sau 2 năm là:
\({\rm{200}}{\rm{.}}{\left( {{\rm{1}} + \frac{{\rm{5}}}{{{\rm{100}}}}} \right)^{\rm{2}}} = {\rm{220}}{\rm{,5}}\) (triệu đồng)
Vậy sau 2 năm người gửi đã nhận số tiền lãi là: \(220,5 - 200 = 20,5\) triệu đồng.
Lời giải
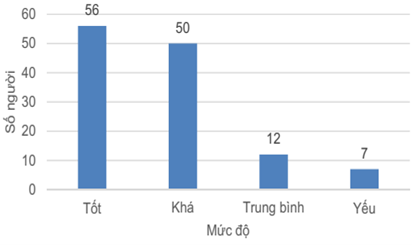
a) Bảng tần số tương đối
|
Mức đánh giá |
Tốt |
Khá |
Trung bình |
Yếu |
|
Tần số tương đối |
44,% |
40% |
9,6% |
5,6% |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.