(2,5 điểm)
Một người gửi 200 triệu vào ngân hàng với lãi suất hàng năm là 5%. Vì bận việc, nên tới ngày nhận lãi năm thứ 2, người đó mới đến ngân hàng nhận lãi. Hỏi người đó đã nhận bao nhiêu tiền lãi (biết lãi suất mỗi năm không đổi)?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 18 !!
Quảng cáo
Trả lời:
Theo công thức lãi kép, số tiền cả vốn lẫn lãi nhận được sau 2 năm là:
\({\rm{200}}{\rm{.}}{\left( {{\rm{1}} + \frac{{\rm{5}}}{{{\rm{100}}}}} \right)^{\rm{2}}} = {\rm{220}}{\rm{,5}}\) (triệu đồng)
Vậy sau 2 năm người gửi đã nhận số tiền lãi là: \(220,5 - 200 = 20,5\) triệu đồng.
Câu hỏi cùng đoạn
Câu 2:
Trong kỳ thi tuyển sinh vào lớp 10 năm học 2023 – 2024, số thí sinh vào trường THPT A bằng 2/3 số thí sinh thi vào trường THPT B. Biết rằng tổng số phòng thi của cả hai trường là 80 phòng và mỗi phòng thi có đúng 24 thí sinh. Tính số thí sinh vào mỗi trường.
Gọi số thí sinh vào trường THPT A và số thí sinh vào trường THPT B lần lượt là \[x,\,y\] (thí sinh) (điều kiện: \[x,\,y \in {\mathbb{N}^*}\]).
Vì số thí sinh vào trường THPT A bằng \[\frac{2}{3}\] số thí sinh vào trường THPT B nên ta có: \[x = \frac{2}{3}y\] (1)
Vì tổng số phòng thi của cả hai trường là 80 phòng và mỗi phòng thi có đúng 24 thí sinh nên tổng số thí sinh của cả hai trường là: \[80.24 = 1920\](thí sinh). Do đó ta có phương trình:
\[x + y = 1920\] (2).
Từ (1) và (2) ta có hệ phương trình
\[\left\{ \begin{array}{l}x = \frac{2}{3}y\\x + y = 1920\end{array} \right.\]
Giải hệ phương trình ta được:
\[\left\{ \begin{array}{l}y = 1152\\x = 768\end{array} \right.{\rm{ (TM)}}\]
Vậy số thí sinh vào trường THPT A và số thí sinh vào trường THPT B lần lượt là 768 thí sinh, 1152 thí sinh.
Câu 3:
Cho phương trình \({x^2} - 6x - 2m + 3 = 0.\) Tìm \[\;m\] để phương trình có hai nghiệm \({x_1},\,\,\,{x_2}\) thỏa mãn \[x_1^2 + x_2^2 = 20.\]
Điều kiện để phương trình có 2 nghiệm là: \(\Delta ' = 2m + 6 \ge 0\) hay \(m \ge - 3.\)
Theo hệ thức Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 6\\{x_1}.{x_2} = - 2m + 3\end{array} \right.\) nên
\(\begin{array}{l}x_1^2 + x_2^2 = 20\\{\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 20\\4m = 10\\m = \frac{5}{2}\,\,\,\left( {TM} \right)\end{array}\)
Vậy \(m = \frac{5}{2}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
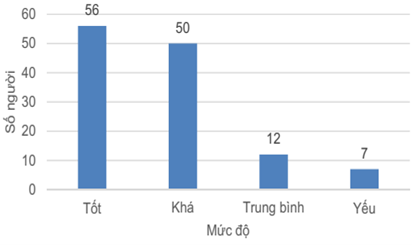
a) Bảng tần số tương đối
|
Mức đánh giá |
Tốt |
Khá |
Trung bình |
Yếu |
|
Tần số tương đối |
44,% |
40% |
9,6% |
5,6% |
Lời giải
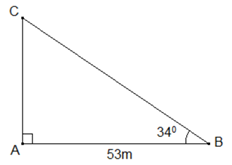
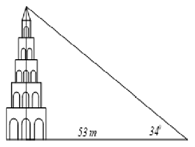
Trong hình vẽ, AC là tòa tháp, AB là bóng của tòa tháp trên mặt đất, \(\widehat B\)là góc tạo bởi tia nắng mặt trời và mặt đất.
Vì \(\Delta ABC\) vuông tại A nên \[AC = AB.\tan B = 53.\tan {34^0} \approx 35,7\,\left( m \right).\]
Vậy chiều cao của tòa tháp khoảng 35,7m.
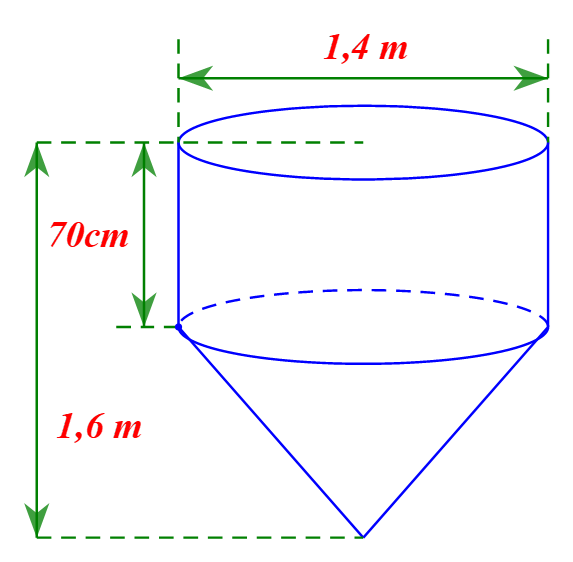
b) Độ dài đường sinh của hình nón là:
\(l = \sqrt {{{0,9}^2} + {{0,7}^2}} = 1,14\,\,\left( m \right).\)
Diện tích xung quanh hình trụ là:
\(2\pi .0,7.0,7 = 0,98\pi \,\,\left( {{m^2}} \right).\)
Diện tích xung quanh của hình nón là:\[\pi .0,7.1,14 = 0,798\pi \,\,\left( {{m^2}} \right).\])
Diện tích mặt ngoài của dụng cụ là: \[0,98\pi + 0,798\pi \, = 1,778\,\pi \,\left( {{m^2}} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.