(4,0 điểm)
Người ta đổ đầy nước vào một bình đong với các kích thước như hình vẽ. Hãy tính thể tích của phần nước trong bình, lấy \[\pi \approx 3,14\](giả sử bề dày của bình đong không đáng kể, kết quả làm tròn đến chữ số thập phân thứ hai).
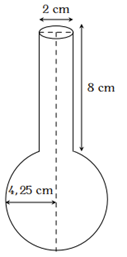
Người ta đổ đầy nước vào một bình đong với các kích thước như hình vẽ. Hãy tính thể tích của phần nước trong bình, lấy \[\pi \approx 3,14\](giả sử bề dày của bình đong không đáng kể, kết quả làm tròn đến chữ số thập phân thứ hai).

Quảng cáo
Trả lời:
Bán kính đáy phần hình trụ là : \[2:1 = 2(cm)\]
Thể tích của phần bình hình trụ là : \[{V_1} = \pi .{r_1}^2.h = {3,14.1^2}.8 = 25,12(c{m^3})\]
Thể tích phần bình hình cầu là: \[{V_2} = \frac{4}{3}\pi .{r_2}^3 = \frac{4}{3}{.3,14.4,25^3} \approx 321,39(c{m^3})\]
Thể tích nước trong bình là : \[V = 25,12 + 321,39 = 346,51(c{m^3})\]
Vậy thể tích nước trong bình khoảng \[346,51(c{m^3})\]
Câu hỏi cùng đoạn
Câu 2:
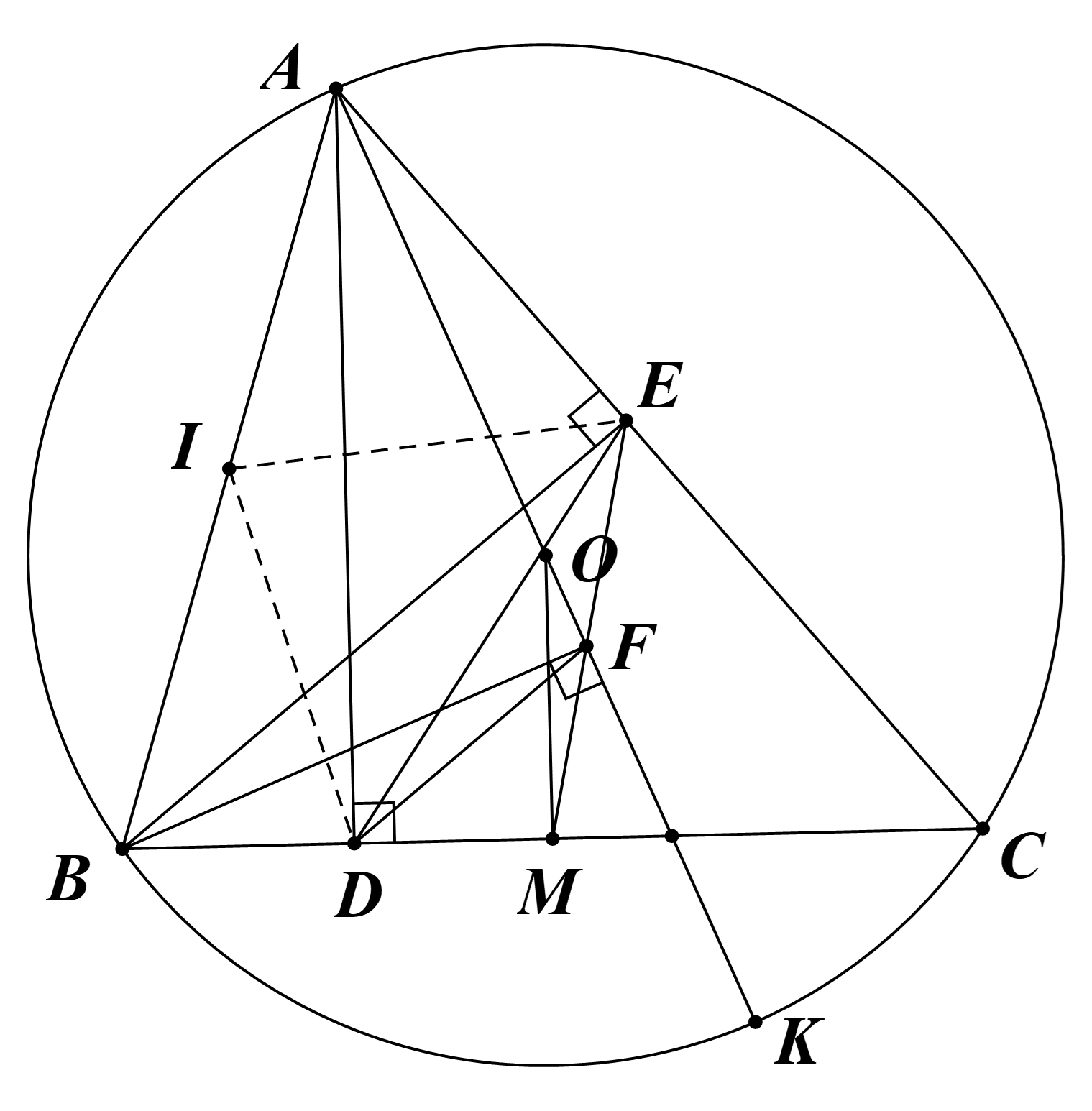
Cho đường tròn \[(O;R)\] và dây \[BC\] cố định không đi qua tâm. Gọi \[A\] là một điểm bất kì trên cung lớn \[BC\] sao cho tam giác \[ABC\] nhọn \[(AB < AC)\]. Kẻ các đường cao \[AD,BE\] của tam giác \[ABC\].
a) Chứng minh: Bốn điểm \[A,E,D,B\] cùng nằm trên một đường tròn.
b) Kẻ đường kính \[AK\] của đường tròn tâm \[O\]. Gọi F là hình chiếu của điểm \[B\] trên \[AK\]. Chứng minh rằng: \[AB.AC = AK.AD\]và \(DF \bot AC\)
c) Gọi \[M\] là trung điểm của \[BC\]. Chứng minh: ba điểm \[E;F;M\] thẳng hàng.
Cho đường tròn \[(O;R)\] và dây \[BC\] cố định không đi qua tâm. Gọi \[A\] là một điểm bất kì trên cung lớn \[BC\] sao cho tam giác \[ABC\] nhọn \[(AB < AC)\]. Kẻ các đường cao \[AD,BE\] của tam giác \[ABC\].
a) Chứng minh: Bốn điểm \[A,E,D,B\] cùng nằm trên một đường tròn.
b) Kẻ đường kính \[AK\] của đường tròn tâm \[O\]. Gọi F là hình chiếu của điểm \[B\] trên \[AK\]. Chứng minh rằng: \[AB.AC = AK.AD\]và \(DF \bot AC\)
c) Gọi \[M\] là trung điểm của \[BC\]. Chứng minh: ba điểm \[E;F;M\] thẳng hàng.
a)
+ Có \[AD\] là đường cao của tam giác \[ABC\]
nên \(AD \bot BC\) \( \Rightarrow \widehat {ADB} = {90^0}\)
+ Có \[BE\] là đường cao của tam giác \[ABC\]
nên \(BE \bot AC\) \( \Rightarrow \widehat {AEB} = {90^0}\)
+ Gọi \[I\] là trung điểm của \[AB\]
\(\Delta ABD\) vuông tại \(D \Rightarrow IA = IB = ID = \frac{{AB}}{2}\) \[(1)\]
\(\Delta ABE\) vuông tại \(E \Rightarrow IA = IB = IE = \frac{{AB}}{2}\) \[(2)\]
Từ \((1);(2)\) suy ra \(IA = IB = IE = ID\left( { = \frac{{AB}}{2}} \right)\)
Nên bốn điểm \(A,B,E,D\) cùng nằm trên một đường tròn .
b) Chứng minh: \[\widehat {ADB} = \widehat {ACK = }{\kern 1pt} \,{90^0}\]
+ Chỉ ra: \[\widehat {ABD} = \widehat {AKC}\]
Chứng minh \(\Delta \)ABD đồng dạng \(\Delta \)AKC (g.g)
và AB.AC = AK.AD
+ Chứng minh tứ giác AFDB nội tiếp
\[ \Rightarrow \widehat {BFD} = \widehat {BAD}\] (1)
+ Vì \(\Delta \)ABD đồng dạng \(\Delta \)AKC
\[ \Rightarrow \widehat {BAD} = \widehat {KAC}\] (2)
+ Chứng minh tứ giác AEFB nội tiếp
\[ \Rightarrow \widehat {EAF} = \widehat {EBF}\]
Hay \[\widehat {CAK} = \widehat {EBF}\] (3)
Từ (1); (2); (3) suy ra: \[\widehat {EBF} = \widehat {BFD}\]
Mà hai góc này ở vị trí so le trong nên BE // DF
Lại có BE \( \bot AC\) (GT)
Vậy DF \( \bot AC\)
c) Gọi M là trung điểm của BC
Suy ra M cố định và OM vuông góc BC (quan hệ giữa đường kính và dây)
+ Chứng minh tứ giác OMBF nội tiếp
Suy ra \[\widehat {OFM} = \widehat {OBM}\,\]
+ Chứng minh \[\widehat {OBM} = \frac{{{{180}^0} - \widehat {BOC}}}{2}\,\, = {90^0} - \widehat {BAC} = \widehat {ABE}\]
Mà \[\widehat {ABE} = \widehat {AFE}\]
nên \[\widehat {AFE} = \widehat {OFM}\]
Từ đó chứng minh \[\widehat {EFM} = {180^0}\]. Suy ra ba điểm E, F, M thẳng hàng
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi khối lượng dung dịch \[HCl\] \[10\% \] là \[x{\rm{ }}(gam,x > 0)\]
Gọi khối lượng dung dịch \[HCl\] \[25\% \] là \[y{\rm{ }}(gam,y > 0)\]
Vì tổng khối lượng hai dung dịch là \[500\] \[gam\] nên ta có phương trình:
\[x + y = 500{\rm{ }}(1)\]
Vì dung dịch tạo thành là \[HCl\] \[16\% \] nên ta có phương trình:
\[10\% x + 25\% y = 16\% .500{\rm{ }}(2)\]
Từ \[(1);{\rm{ }}(2)\] ta có hệ phương trình:
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\10\% x + 25\% y = 16\% .500{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\0,1x + 0,25y = 80{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\x + 2,5y = 800{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x + y = 500{\rm{ }}\\ - 1,5y = - 300{\rm{ }}\end{array} \right.\]
\[\left\{ \begin{array}{l}x = 300{\rm{ }}(tm){\rm{ }}\\y = 200{\rm{ }}(tm){\rm{ }}\end{array} \right.\]
Vậy Bình cần dùng \[300\] \[gam\] dung dịch \[HCl\] \[10\% \] và \[200\]\[gam\] dung dịch \[HCl\] \[25\% \]
Lời giải
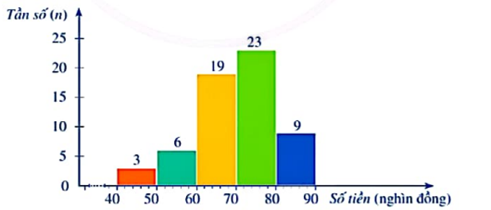
+ Tần số ghép nhóm của nhóm \[\left[ {40;50} \right)\] là \[3\].
+ Tần số tương đối ghép nhóm của nhóm \[\left[ {40;50} \right)\] là: \[\frac{3}{{60}}.100\% = 5\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.