(1,5 điểm)
Ban phụ huynh đặt tặng áo phông cho 40 học sinh của lớp 8A. Ban phụ huynh đo chiều cao (đơn vị: centimét) của cả lớp để quyết định chọn các cỡ áo, kết quả cho bởi bảng tần số ghép nhóm như sau:
Nhóm
\(\left[ {150;155} \right)\)
\(\left[ {155;160} \right)\)
\[\left[ {160;{\rm{ }}165} \right)\]
\[\left[ {165;{\rm{ }}170} \right)\]
\[\left[ {170;{\rm{ }}175} \right)\]
Cộng
Tần số (n)
5
11
12
8
4
N=40
Xác định tần số ghép nhóm và tìm tần số tương đối ghép nhóm của nhóm \[\left[ {160;{\rm{ }}165} \right)\].
Ban phụ huynh đặt tặng áo phông cho 40 học sinh của lớp 8A. Ban phụ huynh đo chiều cao (đơn vị: centimét) của cả lớp để quyết định chọn các cỡ áo, kết quả cho bởi bảng tần số ghép nhóm như sau:
|
Nhóm |
\(\left[ {150;155} \right)\) |
\(\left[ {155;160} \right)\) |
\[\left[ {160;{\rm{ }}165} \right)\] |
\[\left[ {165;{\rm{ }}170} \right)\] |
\[\left[ {170;{\rm{ }}175} \right)\] |
Cộng |
|
Tần số (n) |
5 |
11 |
12 |
8 |
4 |
N=40 |
Xác định tần số ghép nhóm và tìm tần số tương đối ghép nhóm của nhóm \[\left[ {160;{\rm{ }}165} \right)\].
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 29 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dựa vào bảng tần số ghép nhóm đã cho, tần số ghép nhóm của nhóm \[\left[ {160;{\rm{ }}165} \right)\]là 12 và tần số tương đối ghép nhóm của nhóm \[\left[ {160;{\rm{ }}165} \right)\] là \[\frac{{12.100}}{{40}}\% = 30\% \]
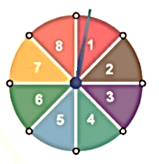
2) Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }} \ldots ;{\rm{ }}8\]. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần.
Tính xác suất của biến cố A: “Chiếc kim chỉ vào hình quạt ghi số lớn hơn 3”.
Câu hỏi cùng đoạn
Câu 2:
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }} \ldots ;{\rm{ }}8\]. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần.
Tính xác suất của biến cố A: “Chiếc kim chỉ vào hình quạt ghi số lớn hơn 3”.
Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }} \ldots ;{\rm{ }}8\]. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần.
Tính xác suất của biến cố A: “Chiếc kim chỉ vào hình quạt ghi số lớn hơn 3”.
Giải bởi Vietjack
Có 5 kết quả thuận lợi cho biến cố A: “Chiếc kim chỉ vào hình quạt ghi số lớn hơn 3” là 4; 5; 6; 7; 8.
Xác suất của biến cố A: “Chiếc kim chỉ vào hình quạt ghi số lớn hơn 3” là: \[\frac{5}{8} = 0,625\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Bán kính đáy của lọ hình trụ là: r = 30:2 = 15 (cm)
Thể tích nước tinh khiết chứa trong lọ bằng thể tích của lọ hình trụ.
Thể tích nước tinh khiết là: \(V = \pi {r_1}^2.{h_1} \approx {3,14.15^2}.20 = 14\,130\) (cm3)
b) Gọi thể tích lọ thứ hai bên trong có đường kính đáy là \(40cm\), chiều cao h2 (cm) là \({V_2}\)
Suy ra \({V_2} = \pi .{r_2}^2.{h_2} \approx 3,14.400.{h_2} = 1\,256.{h_2}\) (cm3)
Theo bài lượng nước trong lọ thứ hai cao một nửa chiều cao của lọ nên: \(1\,256.\frac{{{h_2}}}{2} = 14\,130\)
Suy ra \({h_2} = 22,5\)(cm).
Vậy chiều cao của lọ thứ hai là 22,5 cm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Số tiền của Tuấn mang đến nhà sách là: 300 + 20 = 320 (nghìn đồng)
Gọi số tờ tiền loại 10 nghìn đồng và số tờ tiền loại 20 nghìn đồng lần lượt là \(x\), \(y\) (tờ, \(x,y > 0\))
Vì Tuấn mang 20 tờ tiền nên \(x + y = 20\) (1)
Số tiền của Tuấn mang đến nhà sách là 320 nghìn đồng nên \(10x + 20y = 320\) (2)
Từ (1) và (2) ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 20\\10x + {\rm{20}}y = 320\end{array} \right.\]
Giải hệ trên ta có \(\left\{ \begin{array}{l}x = 8\\y = 12\end{array} \right.\) (thoả mãn).
Vậy lúc đầu Tuấn có 8 tờ tiền loại 10 nghìn đồng và có 12 tờ tiền loại 20 nghìn đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập