Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 29

Dựa vào bảng tần số ghép nhóm đã cho, tần số ghép nhóm của nhóm \[\left[ {160;{\rm{ }}165} \right)\]là 12 và tần số tương đối ghép nhóm của nhóm \[\left[ {160;{\rm{ }}165} \right)\] là \[\frac{{12.100}}{{40}}\%  = 30\% \]

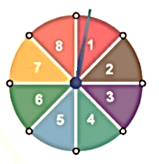
2) Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số \[1;{\rm{ }}2;{\rm{ }}3;{\rm{ }} \ldots ;{\rm{ }}8\]. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần.

Tính xác suất của biến cố A: “Chiếc kim chỉ vào hình quạt ghi số lớn hơn 3”.

2) \(B = \frac{{x + 1}}{{x - \sqrt x }} - \frac{2}{{\sqrt x  - 1}}\) với \(x > 0;x \ne 1\)

\(B = \frac{{x + 1}}{{\sqrt x \left( {\sqrt x  - 1} \right)}} - \frac{{2\sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}}\)

\(B = \frac{{x + 1 - 2\sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}} = \frac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\sqrt x \left( {\sqrt x  - 1} \right)}} = \frac{{\left( {\sqrt x  - 1} \right)}}{{\sqrt x }}\).

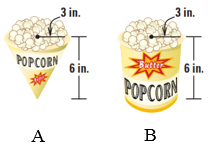
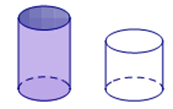
Thể tích hình nón: \[{V_A} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}.\pi {.3^2}.6 = 18\pi \] (in3)

Thể tích hình trụ \[{V_{\bf{B}}} = \pi {r^2}h = \pi {.3^2}.6 = 54\pi \] (in3)

Suy ra \[{V_{\bf{B}}} = 3.{V_A}\]. Do đó, lượng bắp rang bơ trong hộp hình trụ gấp ba lần lượng bắp rang bơ trong hộp hình nón.

Nếu một hộp bắp rang bơ hình nón có giá $1 thì giá tương đương một hộp bắp rang bơ hình trụ có giá là 3.1 = 3 ($).

Để người mua được lợi 10%, thì người mua cần trả 90% nguyên giá, tức là giá sau khi đã giảm là: 90%.3 = 2,7 ($).

Vậy cửa hàng B phải bán với giá $2,7 một hộp (hình trụ) để người mua được lợi 10% so với cùng lượng bắp rang bơ ở cửa hàng A.

Số tiền của Tuấn mang đến nhà sách là: 300 + 20 = 320 (nghìn đồng)

Gọi số tờ tiền loại 10 nghìn đồng và số tờ tiền loại 20 nghìn đồng lần lượt là \(x\), \(y\) (tờ, \(x,y > 0\))

Vì Tuấn mang 20 tờ tiền nên \(x + y = 20\) (1)

Số tiền của Tuấn mang đến nhà sách là 320 nghìn đồng nên \(10x + 20y = 320\) (2)

Từ (1) và (2) ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 20\\10x + {\rm{20}}y = 320\end{array} \right.\]

Giải hệ trên ta có \(\left\{ \begin{array}{l}x = 8\\y = 12\end{array} \right.\) (thoả mãn).

Vậy lúc đầu Tuấn có 8 tờ tiền loại 10 nghìn đồng và có 12 tờ tiền loại 20 nghìn đồng.