(4,0 điểm)
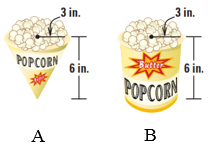
Một lọ thủy tinh hình trụ có đường kính đáy là 30 cm, chiều cao 20 cm, đựng đầy nước tinh khiết.
a. Tính thể tích lượng nước tinh khiết được chứa trong lọ. (Lấy \(\pi \approx 3,14\)).
b. Người ta đổ tất cả lượng nước trên vào một lọ thứ hai bên trong có đường kính đáy là 40 cm thì lượng nước trong lọ thứ hai cao một nửa chiều cao của lọ. Hỏi chiều cao của lọ thứ hai? (Giả sử độ dày của lọ là không đáng kể).
(4,0 điểm)
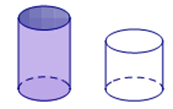
Một lọ thủy tinh hình trụ có đường kính đáy là 30 cm, chiều cao 20 cm, đựng đầy nước tinh khiết.
a. Tính thể tích lượng nước tinh khiết được chứa trong lọ. (Lấy \(\pi \approx 3,14\)).
b. Người ta đổ tất cả lượng nước trên vào một lọ thứ hai bên trong có đường kính đáy là 40 cm thì lượng nước trong lọ thứ hai cao một nửa chiều cao của lọ. Hỏi chiều cao của lọ thứ hai? (Giả sử độ dày của lọ là không đáng kể).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 29 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Bán kính đáy của lọ hình trụ là: r = 30:2 = 15 (cm)
Thể tích nước tinh khiết chứa trong lọ bằng thể tích của lọ hình trụ.
Thể tích nước tinh khiết là: \(V = \pi {r_1}^2.{h_1} \approx {3,14.15^2}.20 = 14\,130\) (cm3)
b) Gọi thể tích lọ thứ hai bên trong có đường kính đáy là \(40cm\), chiều cao h2 (cm) là \({V_2}\)
Suy ra \({V_2} = \pi .{r_2}^2.{h_2} \approx 3,14.400.{h_2} = 1\,256.{h_2}\) (cm3)
Theo bài lượng nước trong lọ thứ hai cao một nửa chiều cao của lọ nên: \(1\,256.\frac{{{h_2}}}{2} = 14\,130\)
Suy ra \({h_2} = 22,5\)(cm).
Vậy chiều cao của lọ thứ hai là 22,5 cm.
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \(\left( O \right)\) và điểm \(M\) ở ngoài đường tròn. Qua \(M\) kẻ các tiếp tuyến \(MA\), \(MB\) và cát tuyến \(MPQ\) (\(MP < MQ\)). Gọi \(I\) là trung điểm của dây \(PQ\).
a. Chứng minh bốn điểm \(B\), \(O\), \(I\), \(M\) cùng thuộc một đường tròn.
b. Gọi \(E\) là giao điểm thứ hai của đường thẳng \(BI\) và đường tròn \(\left( O \right)\).
Chứng minh: \[\widehat {BOM} = \widehat {BEA}\] và \(AE\) song song với \(PQ\).
c. Gọi \(K\) là trung điểm của \(EA\). Chứng minh ba điểm \(O\); \(I\); \(K\) thẳng hàng.
Cho đường tròn \(\left( O \right)\) và điểm \(M\) ở ngoài đường tròn. Qua \(M\) kẻ các tiếp tuyến \(MA\), \(MB\) và cát tuyến \(MPQ\) (\(MP < MQ\)). Gọi \(I\) là trung điểm của dây \(PQ\).
a. Chứng minh bốn điểm \(B\), \(O\), \(I\), \(M\) cùng thuộc một đường tròn.
b. Gọi \(E\) là giao điểm thứ hai của đường thẳng \(BI\) và đường tròn \(\left( O \right)\).
Chứng minh: \[\widehat {BOM} = \widehat {BEA}\] và \(AE\) song song với \(PQ\).
c. Gọi \(K\) là trung điểm của \(EA\). Chứng minh ba điểm \(O\); \(I\); \(K\) thẳng hàng.
Giải bởi Vietjack
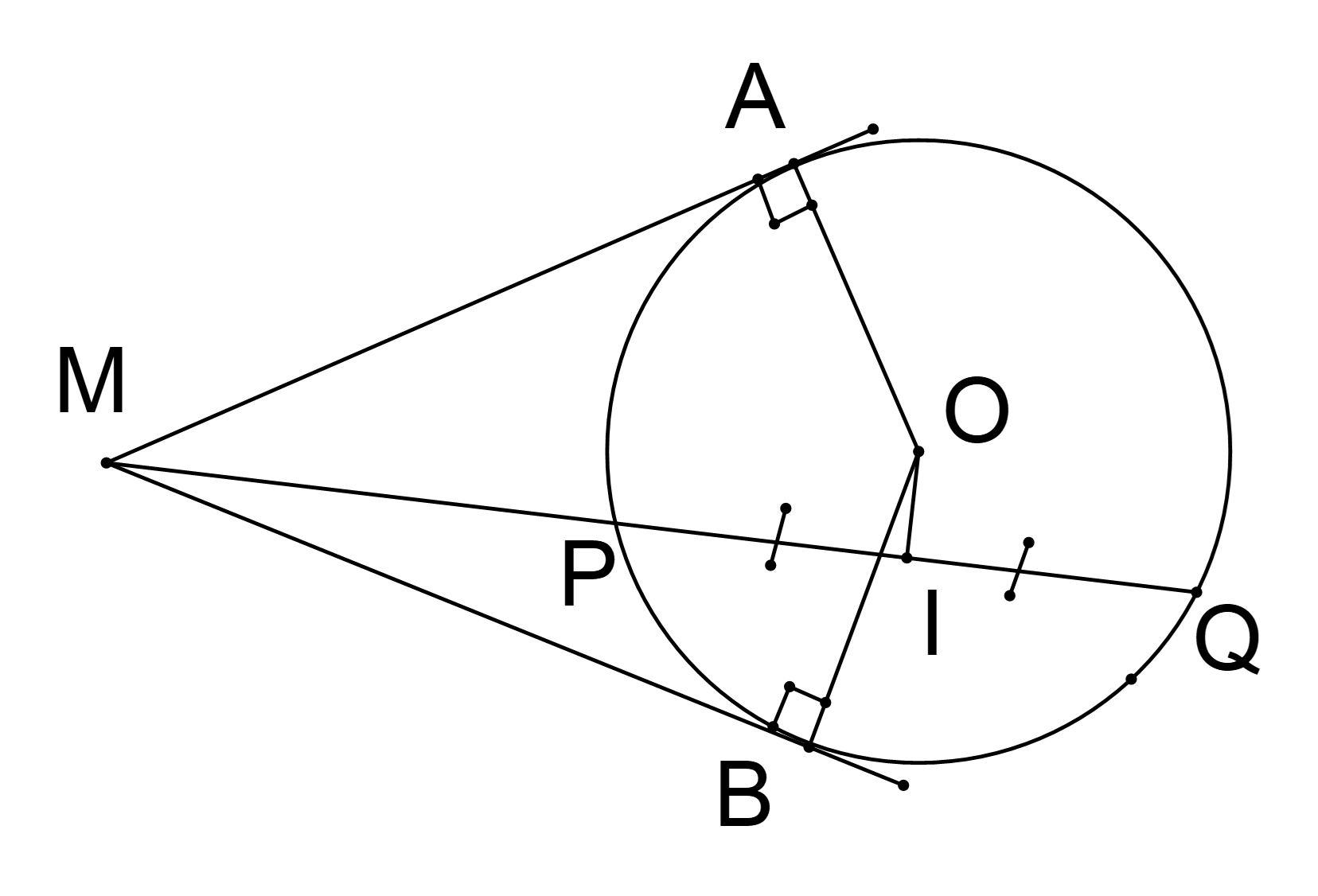
a) +) Có \(MB\) là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(MB \bot OB\) tại \(B\). Suy ra \(B\) thuộc đường tròn đường kính \(MO\) (1)
+) Có \(I\) là trung điểm của dây \(PQ\) của đường tròn \(\left( O \right)\) nên \(OI \bot PQ\) tại \(I\). Suy ra \(I\) thuộc đường tròn đường kính \(MO\) (2)
Từ (1) và (2) suy ra bốn điểm \(B\), \(O\), \(I\), \(M\) cùng thuộc một đường tròn đường kính \(MO\).
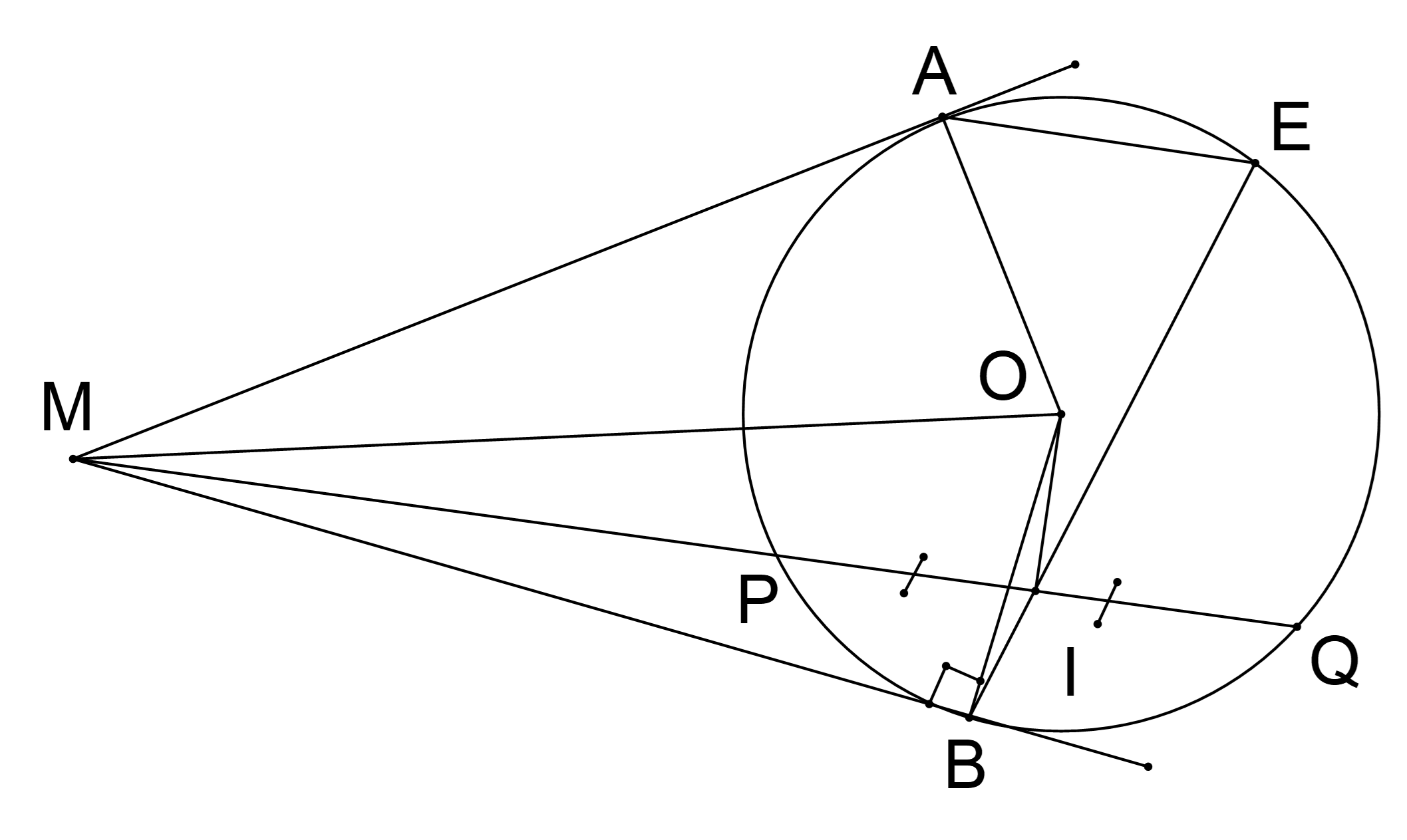
b) +) Xét \(\left( O \right)\) có các tiếp tuyến \(MA\), \(MB\) cắt nhau nên tia \(OM\) là phân giác của \(\widehat {AOB}\).
\[ \Rightarrow \widehat {AOM} = \widehat {BOM} = \frac{1}{2}\widehat {BOA}\]
Lại có \[\widehat {BEA} = \frac{1}{2}\widehat {BOA}\] (góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung)
Suy ra \[\widehat {BOM} = \widehat {BEA}\] (3)
+) Có bốn điểm \(B\), \(O\), \(I\), \(M\) cùng thuộc một đường tròn đường kính \(MO\) (cmt)
\[ \Rightarrow \widehat {BOM} = \widehat {BIM}\] (hai góc nội tiếp cùng chắn một cung ) (4)
Từ (3) và (4) suy ra \[\widehat {BEA} = \widehat {BIM}\].
Mà hai góc này ở vị trí đồng vị nên \(AE\)//\(IM\) hay \(AE\)//\(PQ\).
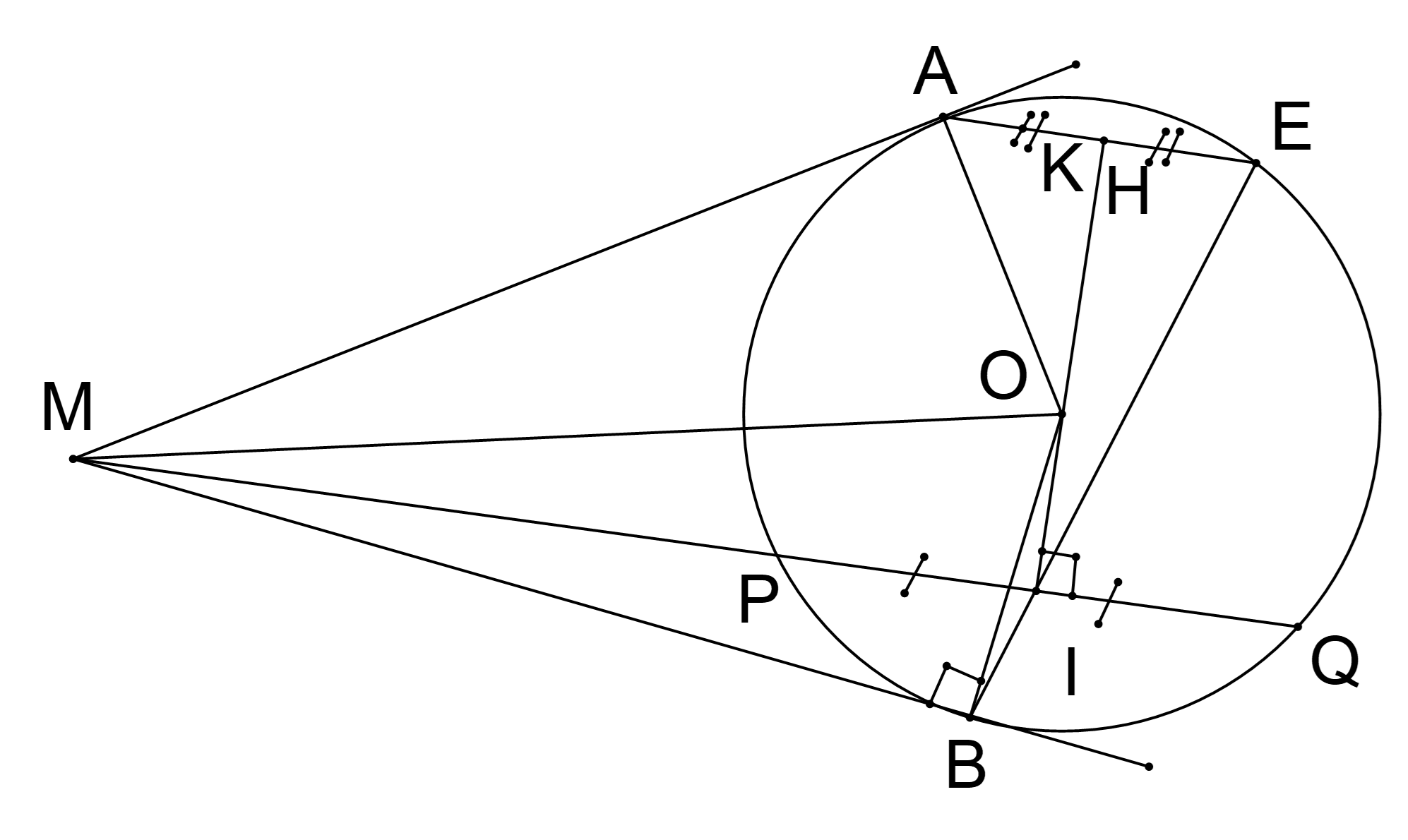
c) Kéo dài \(IO\) cắt \(AE\) tại \(H\).
Do \(OI \bot PQ\) và \(AE\)//\(PQ\) (cmt) nên \(OI \bot AE\) tại \(H\) hay \(OH \bot AE\) tại \(H\).
Suy ra \(H\) là trung điểm của \(AE\).
Mà \(K\) là trung điểm của \(AE\) nên \(K\) và \(H\) trùng nhau.
Suy ra \(K\) thuộc đường thẳng \(OI\).
Vậy ba điểm \(O\); \(I\); \(K\) thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Thay \(x\) = 25 thỏa mãn điều kiện \(x > 0;x \ne 1\) vào biểu thức A, ta được:
\(A = \frac{{\sqrt {25} + 1}}{{\sqrt {25} - 1}} = \frac{{5 + 1}}{{5 - 1}} = \frac{6}{4} = \frac{3}{2}\).
Vậy giá trị của biểu thức A bằng \(\frac{3}{2}\) tại x = 25.
2) \(B = \frac{{x + 1}}{{x - \sqrt x }} - \frac{2}{{\sqrt x - 1}}\) với \(x > 0;x \ne 1\)
\(B = \frac{{x + 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}} - \frac{{2\sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}\)
\(B = \frac{{x + 1 - 2\sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \frac{{\left( {\sqrt x - 1} \right)}}{{\sqrt x }}\).
3) \(P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}.\frac{{\sqrt x - 1}}{{\sqrt x }} = \frac{{\sqrt x + 1}}{{\sqrt x }}\) với \(x > 0;x \ne 1\).
Xét hiệu: \(P - 1 = \frac{{\sqrt x + 1}}{{\sqrt x }} - 1 = \frac{{\sqrt x + 1 - \sqrt x }}{{\sqrt x }} = \frac{1}{{\sqrt x }}\).
Vì \(x > 0\)nên \(\sqrt x > 0\), suy ra \(\frac{1}{{\sqrt x }} > 0\). Do vậy \(P - 1 > 0 \Rightarrow P > 1\).
Vậy \(P > 1\).
Lời giải
Số tiền của Tuấn mang đến nhà sách là: 300 + 20 = 320 (nghìn đồng)
Gọi số tờ tiền loại 10 nghìn đồng và số tờ tiền loại 20 nghìn đồng lần lượt là \(x\), \(y\) (tờ, \(x,y > 0\))
Vì Tuấn mang 20 tờ tiền nên \(x + y = 20\) (1)
Số tiền của Tuấn mang đến nhà sách là 320 nghìn đồng nên \(10x + 20y = 320\) (2)
Từ (1) và (2) ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 20\\10x + {\rm{20}}y = 320\end{array} \right.\]
Giải hệ trên ta có \(\left\{ \begin{array}{l}x = 8\\y = 12\end{array} \right.\) (thoả mãn).
Vậy lúc đầu Tuấn có 8 tờ tiền loại 10 nghìn đồng và có 12 tờ tiền loại 20 nghìn đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập