(2,5 điểm)
Mai mua hai loại hàng và phải trả tổng cộng 165000 đồng, trong đó đã tính 15000 đồng là thuế giá trị gia tăng (viết tắt là VAT). Biết rằng thuế VAT với loại hàng thứ nhất là 12%; thuế VAT với loại hàng thứ hai là 9%. Hỏi nếu không kể thuế thì Mai phải trả bao nhiêu tiền cho mỗi loại hàng?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 30 !!
Quảng cáo
Trả lời:
Gọi \(x\), \(y\) (đồng ) lần lượt là số tiền của loại hàng thứ nhất và loại hàng thứ hai không kể thuế VAT mà Mai đã mua (\(x,y > 0\))
Số tiền khi mua loại hàng thứ nhất sau khi tính thuế là: \(x + 12\% x = 1,12x\) (đồng).
Số tiền khi mua loại hàng thứ hai sau khi tính thuế là: \(y + 9\% y = 1,09y\) (đồng).
Tổng số tiền khi mua hai loại hàng sau khi tính thuế là 165000 đồng ta có phương trình:
\(1,12x + 1,09y = 165000\) (1)
Tổng số tiền thuế của hai loại hàng là 10000 đồng ta có phương trình:
\(12\% x + 9\% y = 15000\)
Hay \(0,12x + 0,09y = 15000\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}1,12x + 1,09y = 165000\\0,12x + 0,09y = 15000\end{array} \right.\)
Giải hệ ta có: \(\left\{ \begin{array}{l}x = 50000\\y = 100000\end{array} \right.\)(thỏa mãn)
Vậy số tiền không kể thuế của loại hàng thứ nhất là 50000 đồng, số tiền không kể thuế của loại hàng thứ hai là 100000 đồng.
2) Hưởng ứng phong trào thi đua “Xây dựng trường học thân thiệnCâu hỏi cùng đoạn
Câu 2:
Hưởng ứng phong trào thi đua “Xây dựng trường học thân thiện, học sinh tích cực”, lớp 9A trường THCS Hoàng Hoa Thám dự định trồng 300 cây xanh. Đến ngày lao động, có 5 bạn được Liên Đội triệu tập tham gia chiến dịch an toàn giao thông nên mỗi bạn còn lại phải trồng thêm 2 cây mới đảm bảo kế hoạch đặt ra. Hỏi lớp 9A có bao nhiêu học sinh?
Gọi số HS lớp 9A là \(x\) ( học sinh), \(x \in \mathbb{N},x > 5\)
Số học sinh thực tế tham gia trồng cây là : \(x - 5\)( học sinh)
Theo kế hoạch mỗi học sinh phải trồng số cây là: \(\frac{{300}}{x}\) (cây)
Thực tế, mỗi học sinh phải trồng số cây là: \(\frac{{300}}{{x - 5}}\) (cây)
Vì thực tế mỗi học sinh phải trồng thêm 2 cây so với kế hoạch nên ta có phương trình:
\(\begin{array}{l}\frac{{300}}{{x - 5}} - \frac{{300}}{x} = 2\\{x^2} - 5x - 750 = 0\end{array}\)
Giải phương trình ta được: \({x_1} = 30\)(thoả mãn); \({x_2} = - 25\)(loại)
Vậy lớp 9A có 30 học sinh.
Câu 3:
Cho phương trình: \({x^2} - 3x - {m^2} + 1 = 0\) (m là tham số) (1) Tìm m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\)thỏa mãn \(\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) = 1\)
Cho phương trình: \({x^2} - 3x - {m^2} + 1 = 0\) (m là tham số) (1) Tìm m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\)thỏa mãn \(\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) = 1\)
Ta có: \({x^2} - 3x - {m^2} + 1 = 0\) \(\left( 1 \right)\)
Phương trình có \(\Delta = {b^2} - 4ac = 9 - 4\left( { - {m^2} + 1} \right) = 4{m^2} + 5 > 0\)mọi \(m\)
Do đó phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt với mọi \(m\)
Theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + x{}_2 = 3\\{x_1} + {x_2} = - {m^2} + 1\end{array} \right.\)
Theo đề bài ta có \(\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) = 1\)
\({x_1}{x_2} + {x_1} + {x_2} = 0\)
\( - {m^2} + 1 + 3 = 0\)
\({m^2} = 4\)
\(m = \pm 2\)
Kết hợp với điều kiện, ta được \(m = \pm 2\) là giá trị cần tìm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ký hiệu độ dài đường sinh của hình nón là \(l\), bán kính đáy nón là \[r\].
Độ dài đường sinh bằng \(l = \sqrt {{h^2} + {r^2}} = \sqrt {{{16}^2} + {{12}^2}} = 20\)(cm).
Ta có \({S_{xq}} = \pi rl = \pi .12.20 \approx 240.3,14 \approx 754(c{m^2})\).
Lời giải
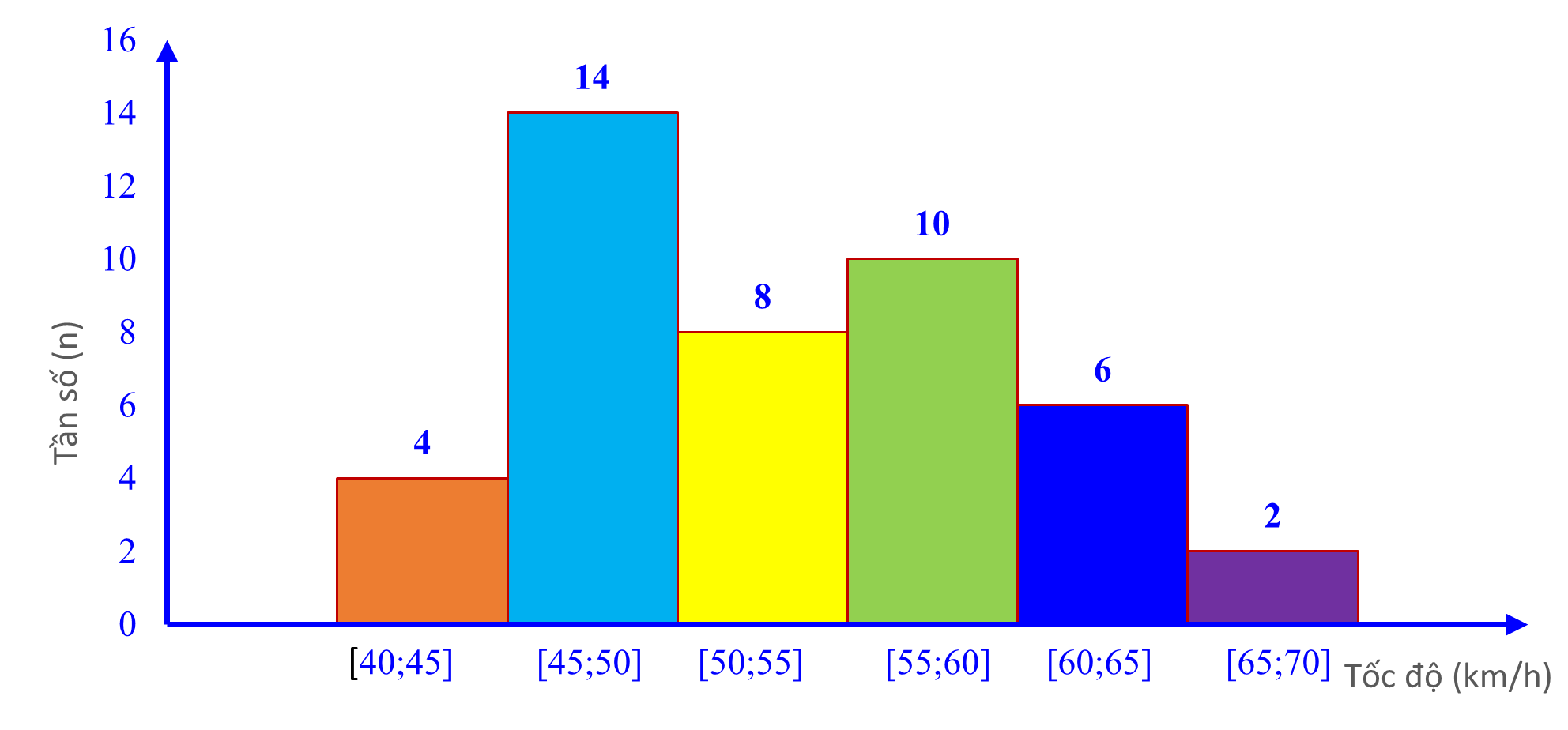
Số lượng ô tô ở nhóm [45;50] là nhiều nhất : 14 chiếc
Tần số tương đối của nhóm là \(\frac{{14.100}}{{44}}\)% \( \approx 31,8\)%
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.