(4 điểm)
Một hình nón có chiều cao \[h{\rm{ = }}16\] cm và bán kính đường tròn đáy \[r{\rm{ }} = {\rm{ }}12\]cm. Tính độ dài đường sinh và diện tích xung quanh của hình nón đó. (Tính với số \(\pi \approx 3,14\)và kết quả làm tròn đến chữ sô hàng đơn vị)
Quảng cáo
Trả lời:
Ký hiệu độ dài đường sinh của hình nón là \(l\), bán kính đáy nón là \[r\].
Độ dài đường sinh bằng \(l = \sqrt {{h^2} + {r^2}} = \sqrt {{{16}^2} + {{12}^2}} = 20\)(cm).
Ta có \({S_{xq}} = \pi rl = \pi .12.20 \approx 240.3,14 \approx 754(c{m^2})\).
Câu hỏi cùng đoạn
Câu 2:
Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\), các đường cao \(AD\), \(BE\), \(CF\) cắt nhau tại \(H\). Kẻ đường kính \(AQ\) của đường tròn \(\left( O \right)\) cắt cạnh \(BC\) tại \(I\).
a) Chứng minh bốn điểm \(A\), \(F\), \(H\), \(E\) cùng thuộc một đường tròn.
b) Chứng minh \(\widehat {BAD} = \widehat {CAQ}\).
c) Gọi \(P\) là giao điểm của \(AH\) và \(EF\). Chứng minh \(\Delta AEP\)đồng dạng với \(\Delta ABI\) và \(PI\) song song với \(HQ\).
Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\), các đường cao \(AD\), \(BE\), \(CF\) cắt nhau tại \(H\). Kẻ đường kính \(AQ\) của đường tròn \(\left( O \right)\) cắt cạnh \(BC\) tại \(I\).
a) Chứng minh bốn điểm \(A\), \(F\), \(H\), \(E\) cùng thuộc một đường tròn.
b) Chứng minh \(\widehat {BAD} = \widehat {CAQ}\).
c) Gọi \(P\) là giao điểm của \(AH\) và \(EF\). Chứng minh \(\Delta AEP\)đồng dạng với \(\Delta ABI\) và \(PI\) song song với \(HQ\).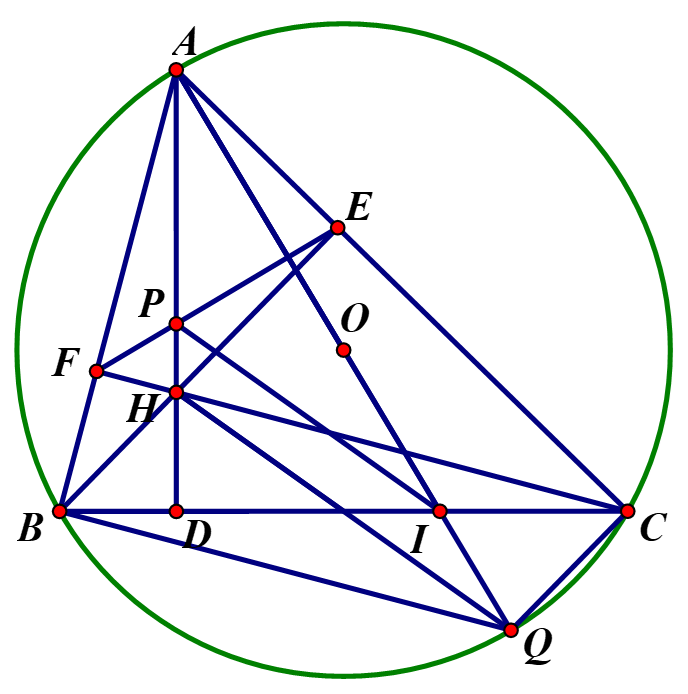
a) Ta có \(BE\)\( \bot \) \(AC\)(gt) nên \(\widehat {AEH} = {90^0}\). Suy ra \(\Delta AEH\)vuông tại \(E\).
Suy ra \(A\), \(H\), \(E\) cùng thuộc đường tròn đường kính \(AH\) (1)
Ta có \(CF\)\( \bot \) \(AB\) (gt) nên \(\widehat {HFA} = {90^0}\). Suy ra \(\Delta AFH\) vuông tại \(F\).
Suy ra \(A\), \(H\), \(F\) cùng thuộc đường tròn đường kính \(AH\) (2)
Từ (1), (2) suy ra bốn điểm \(A\), \(F\), \(H\), \(E\) cùng thuộc đường tròn đường kính \(AH\).
b) Xét đường tròn \(\left( O \right)\) có:
\(\widehat {ABC} = \widehat {AQC}\) (hai góc nội tiếp cùng chắn cung )
\(\widehat {ACQ} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
Xét \(\Delta ADB\) và \(\Delta ACQ\) có: \(\widehat {ABC} = \widehat {AQC}\); \(\widehat {ADB} = \widehat {ACQ} = {90^0}\).
Suy ra \[\Delta ADB \sim \Delta ACQ\]. Suy ra \(\widehat {BAD} = \widehat {CAQ}\).
c) Vì \(\widehat {BAD} = \widehat {CAQ}\) nên \(\widehat {BAD} + \widehat {DAQ} = \widehat {DAQ} + \widehat {QAC}\).
Suy ra \(\widehat {BAI} = \widehat {PAE}\).
Chứng minh \(\Delta AEP\) đồng dạng với \(\Delta ABI\)(g.g). Từ đó suy ra \(\frac{{AE}}{{AB}} = \frac{{AP}}{{AI}}\) (3)
Chứng minh \(\Delta AEH\) đồng dạng với \(\Delta ABQ\)(g.g). Từ đó suy ra \(\frac{{AE}}{{AB}} = \frac{{AH}}{{AQ}}\) (4)
Từ (3) và (4) suy ra \(\frac{{AP}}{{AI}} = \frac{{AH}}{{AQ}}\) hay \(\frac{{AP}}{{AH}} = \frac{{AI}}{{AQ}}\).
Suy ra \(PI\) song song với \(HQ\) (định lý Thales đảo).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\), \(y\) (đồng ) lần lượt là số tiền của loại hàng thứ nhất và loại hàng thứ hai không kể thuế VAT mà Mai đã mua (\(x,y > 0\))
Số tiền khi mua loại hàng thứ nhất sau khi tính thuế là: \(x + 12\% x = 1,12x\) (đồng).
Số tiền khi mua loại hàng thứ hai sau khi tính thuế là: \(y + 9\% y = 1,09y\) (đồng).
Tổng số tiền khi mua hai loại hàng sau khi tính thuế là 165000 đồng ta có phương trình:
\(1,12x + 1,09y = 165000\) (1)
Tổng số tiền thuế của hai loại hàng là 10000 đồng ta có phương trình:
\(12\% x + 9\% y = 15000\)
Hay \(0,12x + 0,09y = 15000\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}1,12x + 1,09y = 165000\\0,12x + 0,09y = 15000\end{array} \right.\)
Giải hệ ta có: \(\left\{ \begin{array}{l}x = 50000\\y = 100000\end{array} \right.\)(thỏa mãn)
Vậy số tiền không kể thuế của loại hàng thứ nhất là 50000 đồng, số tiền không kể thuế của loại hàng thứ hai là 100000 đồng.
2) Hưởng ứng phong trào thi đua “Xây dựng trường học thân thiệnLời giải
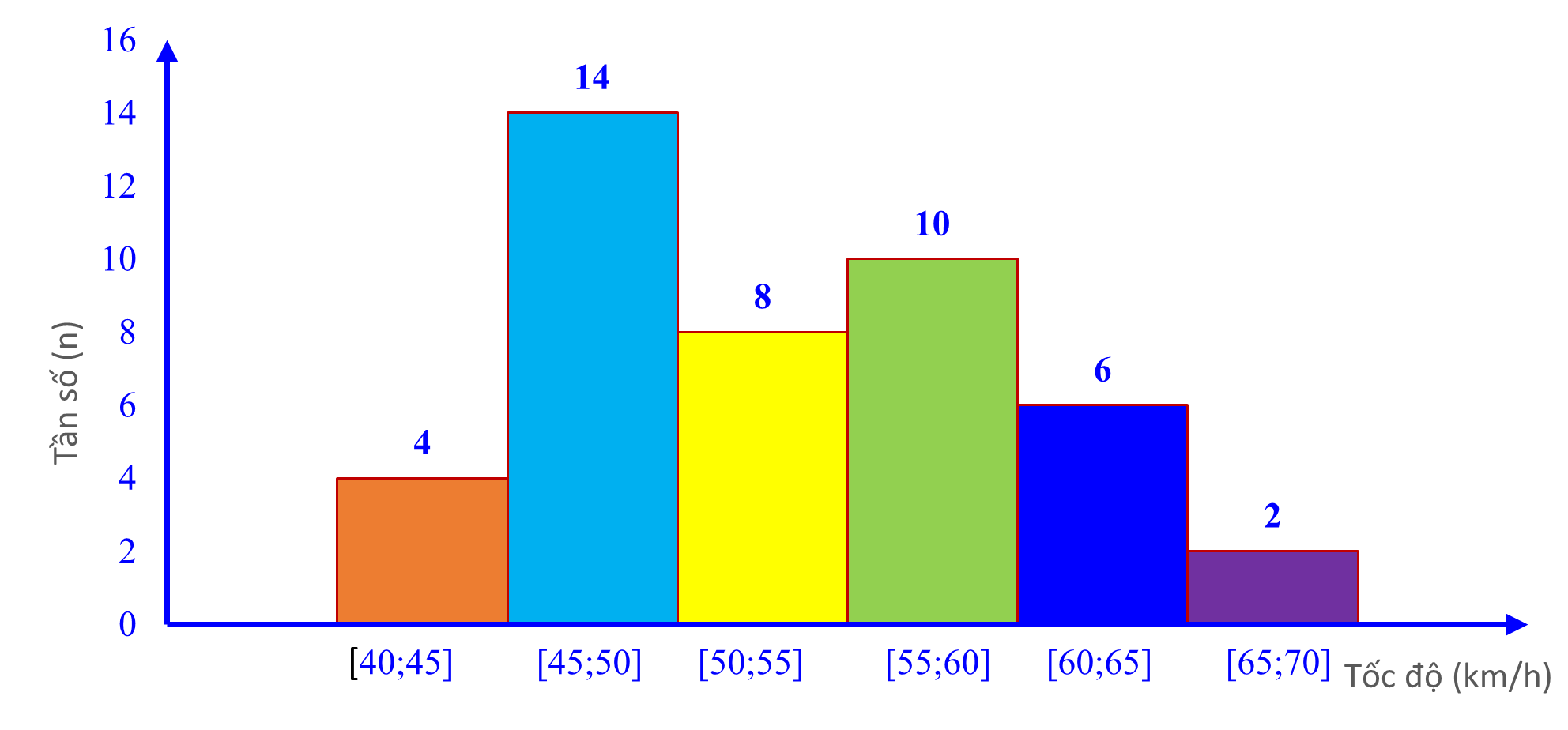
Số lượng ô tô ở nhóm [45;50] là nhiều nhất : 14 chiếc
Tần số tương đối của nhóm là \(\frac{{14.100}}{{44}}\)% \( \approx 31,8\)%
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.