(2,5 điểm)
Có hai loại dung dịch acid cùng loại có nồng độ acid lần lượt là \[10\% \] và \(20\% \), trộn hai dung dịch acid đó để được \(0,5\)\({\rm{kg}}\) dung dịch có nồng độ acid là \(16\% \). Tính cần dùng bao nhiêu \({\rm{gam}}\) mỗi loại dung dịch acid nói trên.
Quảng cáo
Trả lời:
Đổi \(0,5\,{\rm{kg}} = 5{\rm{00}}\,{\rm{g}}\)
Gọi khối lượng dung dịch acid có nồng độ \[10\% \] đem trộn là \[x\]\[\left( {\rm{g}} \right)\]\[\left( {0 < x < 500} \right)\].
Gọi khối lượng dung dịch acid có nồng độ \(20\% \) đem trộn là \[y\]\[\left( {\rm{g}} \right)\]\[\left( {0 < y < 500} \right)\].
Vì trộn \[x\]\[\left( {\rm{g}} \right)\] dung dịch acid có nồng độ \[10\% \] và \[y\]\[\left( {\rm{g}} \right)\] dung dịch acid loại có nồng độ \(20\% \) để được \(500\)\({\rm{kg}}\) acid mới nên ta có phương trình: \[x + y = 500\] (1)
Vì trộn hai loại dung dịch acid cùng loại có nồng độ acid lần lượt là \[10{\raise0.5ex\hbox{$\scriptstyle 0$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 0$}}\] và \(20\% \) để được \(0,5\)\({\rm{kg}}\) dung dịch có nồng độ acid là \(16\% \)nên ta có phương trình:
\[10\% x + 20\% y = 16\% \,\,.\,\,500\]
\[0,1x + 0,2y = 80\] (2)
Từ (1) và (2) ta có hệ phương trình:
\[\left\{ {\begin{array}{*{20}{c}}{0,1x + 0,2y = 80\,\,\,\,\,\,\,\left( 1 \right)}\\{x + y = 500\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\]
Từ \[\left( 2 \right)\] suy ra \[y = 500 - x\,\,\,\,\,\,\left( 3 \right)\]
Thay \[\left( 3 \right)\] vào \[\left( 1 \right)\] ta được \[0,1x + 0,2\,\left( {500 - x} \right) = 80\]
\[0,1x + 100 - 0,2x = 80\]
\[ - 0,1x = - 20\]
\[x = 200\] (nhận)
Thay \[x = 200\] vào \[\left( 3 \right)\] ta được \[y = 300\,\](nhận)
Vậy khối lượng dung dịch acid loại có nồng độ acid \[10\% \]là \[20\,0\,{\rm{g}}\].
Khối lượng dung dịch acid loại có nồng độ acid \(20\% \)là \[300\,{\rm{g}}\].
Câu hỏi cùng đoạn
Câu 2:
Xe máy thứ nhất đi quãng đường từ Hà Nội về Nam Định hết \(3\) giờ \(20\) phút. Xe máy thứ hai đi hết \(3\) giờ \(40\) phút. Mỗi giờ xe máy thứ nhất đi nhanh hơn xe thứ hai là \(3\,\,{\rm{km}}\). Tính vận tốc của mỗi xe máy và quãng đường từ Hà Nội về Nam Định.
- Gọi vận tốc của xe máy thứ nhất và xe máy thứ hai lần lượt là \({\rm{x}}\,{\rm{,}}\,\,{\rm{y}}\,\,\left( {{\rm{km/h}}} \right)\,\), \({\rm{x}}\,{\rm{ > }}\,3\), \({\rm{y > }}\,0\).
- Vì xe thứ nhất đi nhanh hơn xe thứ hai là \(3\,\,{\rm{km/h}}\) nên ta có: \(x\, - \,y\, = \,3\,\,\,\,\,\,\,\,\left( 1 \right)\)
- Trong \(3\) giờ \(20\) phút = \(\frac{{10}}{3}\,\,{\rm{h}}\), xe máy thứ nhất đi được : \(\frac{{10}}{3}x\,\,\left( {{\rm{km}}} \right)\)
- Trong \(3\) giờ \(40\) phút = \(\frac{{11}}{3}\,\,{\rm{h}}\), xe máy thứ hai đi được : \(\frac{{11}}{3}{\rm{y}}\,\,\left( {{\rm{km}}} \right)\)
- Đó là quãng đường từ Hà Nội đến Nam Định nên ta có phương trình:
\(\begin{array}{l}\frac{{10}}{3}x\,\, = \frac{{11}}{3}y\\\frac{{10}}{3}x\,\, - \frac{{11}}{3}y\,\, = \,\,0\,\,\,\,\,\,\,\,\,{\rm{ }}\left( 2 \right)\end{array}\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình:
Vậy vận tốc của xe máy thứ nhất là \(33\,\,\left( {{\rm{km/h}}} \right)\) và vận tốc xe máy thứ hai \(30\,\,\left( {{\rm{km/h}}} \right)\)
Quãng đường từ Hà Nội đến Nam Định là: \(\frac{{10}}{3}\,\,.\,\,33 = 110\,\,\left( {{\rm{km}}} \right)\).
Câu 3:
Cho phương trình: \[{x^2}--\left( {4m--1} \right)x + 3{m^2}--2m = 0\] (ẩn\[x\]). Tìm \[m\]để phương trình có hai nghiệm phân biệt \[{x_1},{x_2}\]thỏa mãn điều kiện : \(x_1^2 + x_2^2 = 7\).
Phương trình đã cho có \[\Delta = {\left( {4m{\rm{ }}--{\rm{ }}1} \right)^2}--{\rm{ }}12{m^2} + {\rm{ }}8m{\rm{ }} = {\rm{ }}4{m^2} + {\rm{ }}1{\rm{ }} > {\rm{ }}0\], \[\forall m\].
Vậy phương trình có 2 nghiệm phân biệt \[\forall m\].
+ Theo ĐL Vi –ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4m - 1\\{x_1}{x_2} = 3{m^2} - 2m\end{array} \right.\).
Khi đó: \(x_1^2 + x_2^2 = 7\)
\({({x_1} + {x_2})^2} - 2{x_1}{x_2} = 7\)
\[{\left( {4m--1} \right)^2}--2\left( {3{m^2}--2m} \right) = 7\]
\[10{m^2}--4m--6 = 0\]
\[5{m^2}--2m--3 = 0\]
Ta thấy tổng các hệ số: a + b + c = 0 suy ra \[m = 1,\,\,m = - \frac{3}{5}\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Thể tích của quả dưa hấu hình vuông là:
\({V_1} = {18^3} = 5832\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
b) Thể tích của một miếng dưa hấu nhỏ hình vuông có cạnh \(5\)cm là:
\({V_2} = {5^3} = 125\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
Số miếng dưa nhỏ được cắt ra là: \(5832\,:\,125 = 46,656\) ( miếng)
Số đĩa dưa mà bạn Minh có thể xếp được là: \(46,656\,:\,12 \approx 4\) (đĩa).
Lời giải
a) \[\Omega = \left\{ {10\;;\,\,11\;;\;\,12\;;\;\,13\;;\;\,...\;;\,\;98\;;\;\,99} \right\}\]
b) Kết quả thuận lợi cho biến cố \(B:\) “Số tự nhiên được viết ra chia hết cho \[11\]” là:
\[11\;;\,\,22\;;\,\,33\;;\;\,44\;;\;\,55\;;\;\,66\;;\;\,77\;;\;\,88\;;\;\,99\]
c) Kết quả thuận lợi cho biến cố \(C\): “Số tự nhiên được viết ra chia cho \[10\] dư \[6\]” là:
\[16\;;\;26\;;\;\,36\;;\;\,46\;;\;\,56\;;\;\,76\;;\;\,86\;;\;\,96\]
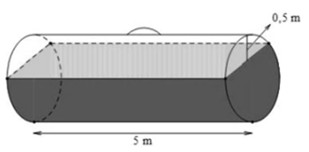
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.